前面推导出了单质点系由速度和位移激励的动力平衡方程及相应的反应谱求解方法，其推导在数学上是严格的，证明该方法在理论上是正确的，而且也得到了实际应用。现在来解决多质点系的问题。

各质点产生的惯性力为

阻尼力则为

弹性恢复力为

因此运动平衡方程可表示为

将式（5-102）～式（5-104）代入式（5-105）后有

即

上述各式中n表示质点个数。

式（5-106）可用矩阵形式表示为

式中：[M]、[C]、[K]依次为质量矩阵、阻尼矩阵、刚度矩阵。

式（5-107）就是多质点系在地震动速度和位移激励下的动力平衡方程。

（2）多质点系爆破地震动位移和速度激励的动力平衡方程的求解方法。

1）阻尼矩阵的处理。仍如前述 （5.1节）地震动加速度激励的方程一样，采用瑞利阻尼，假定阻尼系数矩阵[C]是质量矩阵[M]与刚度矩阵[K]的线性组合[1]，即ci=α1mi

具体计算时，组合系数α1及α2的确定方法与第7章所述完全相同。

2）振型分解法。根据结构动力学原理，利用振型坐标的正交性，将多质点系振动平衡方程分解为n个互不耦联的方程，再分别求解各主坐标的动力平衡方程。

根据多自由度体系的绝对几何坐标与振型正则坐标的变换关系：

这就是第5.1节讨论的以加速度激励的平衡方程，可见二者是可以互换的，其求解方法，在第5.1节已讨论过了。这里要推导出求解以速度、位移激励的动力平衡方程的方法。

式（5-111）左边乘以｛φj｝T，并根据振型的正交性，有

同样也有

将式（5-112）及式（5-113）的结果代入式（5-111）后可得

用｛φj｝T[M]｛φj｝除式（5-114）各项，并引入

则式（5-114）可写成

令

称qaj（t）为绝对正则坐标，以区别正则坐标qj（t）。分别对式（5-117）微分一次和两次，可得绝对正则坐标的速度和加速度如下：

于是式（5-116）可改写为

这样，原几何坐标的运动微分方程组分解成n个独立绝对正则坐标qaj（t）的微分方程，各阶可以独立求解。每一阶振型都有同样的这种方程，只要把方程中的频率ωj、阻尼系数、振型参与系数rj换成相应振型的即可。为便于求解，引进阻尼比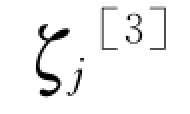，即

方程（5-119）写成标准形式：

其解法仍可按照单质点系振动方程求解的方法，用杜哈姆积分计算出qaj（t），即

几何坐标系统的结构系统各质点相对位移可按式（5-124）确定：

或

相对速度和相对加速度则分别以以下形式表示：

或

各质点i的绝对位移、绝对速度和绝对加速度，则由相对位移等代入式（5-109）可得：

由上述结果可以看出，此方法求解与用加速度作为激励的求解方法不同之处是引入了绝对正则坐标的概念，它与通常的正则坐标qj（t）的关系可由式（5-123）所表示。用式（5-122）求出绝对正则坐标后，必须通过式（5-123）变换为通常的正则坐标，再求得几何坐标的相对位移等。几何坐标下的绝对位移等则由式（5-127）计算。

（3）多质点系爆破地震动速度和位移激励的振动响应的反应谱方法。

下面主要介绍水平地面运动速度作用下的反应谱求解方法。

1）加速度反应谱法。根据多质点结构体系的动力特性，它的每一个振型，都可以用前述方法求得一个独立的单自由度方程。这种独立方程就是用正则坐标确立的方程，它们把几个联立微分方程变换为了几个独立的即互不耦联的方程，可以用单自由度方法求解出正则坐标的反应，即前述的振型分解法；再把各振型的反应变换到几何坐标的反应，这就是振型叠加法。

由于求各阶正则坐标的杜哈姆积分，可得出全过程的反应，但往往只对其最大反应感兴趣，因此就可以只取整个过程的最大反应，建立反应谱曲线，对工程应用来说是很有效的方法。

多质点弹性体系在爆破地震的作用下，在每一个质点上产生的惯性力可以分别求各阶振型的每一个质点的惯性力，再用常规方法求得多质点结构体系每一阶振型效应，按照振型叠加原理，求得多质点结构体系的动力反应。用反应谱方法，求得的是每一阶的每一个质点上的作用（即惯性力）均是振动过程中的最大值。

假令在质点i上产生的地震作用等于质点i上的惯性力

即求

的两次微分，应由第4章式（4-30），式 （4-31）求得，于是式（5-129）可表示为

如第5.1节一样，可以证明

将式（5-131）代入式（5-130），得(www.daowen.com)

由此可见，爆破地震对于第j阶振型，质点i产生的作用力，即荷载为

应用反应谱理论，引进反应谱动力放大系数，将式（5-134）变换为

根据加速度反应谱的定义，有

βaj称为绝对加速度比值反应谱值，也称动力放大系数。

于是式（5-135）可写成式（5-137）：

式中：Wi为质点i的重量；g为重力加速度，取9.81m/s2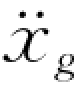；为爆破地震动加速度最大值；βaj称为爆破地震加速度比值反应谱值；φij为第j阶振型在质点i处的相对位移振幅值；rj为第j阶振型参与系数。

把各阶振型的每一个质点的惯性力求出后，就可能按一般结构静力学方法求结构的响应 （变形、弯矩、轴力、剪力）。由于用振型分解反应谱法求出的各阶振型的作用FIij都是最大值，各振型的响应也肯定是最大值。而各振型的响应不会同时发生，因此不能直接把各质点i的各振型地震作用都加起来，这里显然有一个组合问题。为此，先分别求各阶振型地面运动作用下的结构振动响应。用Sj表示第j阶振型的响应（j=1，2，…，n），把每一阶的响应都求出后，再把各阶振型的响应组合起来，就可求得总的响应。根据概率论的分析，对于天然地震作用，认为用“平方和开平方”的方法组合，近似性较好。所谓“平方和”，即是把各阶振型的响应平方后再加起来。“开平方”，即把各阶响应平方之和，即加起来的结果，再开平方。这样的结果就作为地震作用的响应，即

S表示水平地震作用的结构总的响应，Sj表示第j阶振型水平地震作用产生的响应。通常对天然地震由于结构自振频率与地震主频较为接近，一般只要取前3阶，多则取前5阶就可以满足精度要求了。但对于爆破地震主频率较高的情况，计算时取的阶数要增加。取到多少阶更合适，一般应为使计算所取的结构振型频率等于高于地震波主频的那一阶数就可以了。也就是说，所取的各阶振型的反应谱动力的放大系数βaj包含有最大值βmax时，所取的振型数就够了。从这个意义上说，爆破地震作用对通常结构的效应相当于天然地震作用对长周期高柔结构的效应。对爆破地震来说，通常的结构就是长周期结构了。

2）位移反应谱方法。对于工程爆破地震，常用地面振动速度衡量地面运动的强弱程度，并用振速作为评价安全的标准。对爆破工程地震动的监测也多测定地面或建筑结构的振动速度。因此直接应用振动速度确定爆破地震工程结构的荷载，是顺理成章的。

位移反应谱计算爆破地震动荷载。

质点i在第j阶振型的地震惯性力等于质点i在第j阶振型时的弹性抗力，假定忽略阻尼力的情况下，有

式中：Fij为质量mi的质点在第j阶振型的地震力；ωj为第j阶振型的圆频率；uij（t）为质点i在第j阶振型时的位移。

在前面已讨论过多自由度体系振动问题分解成对每一个振型单独作为一个自由度问题来处理，即把复杂的多质点结构的振动，分解成各个振型的独立振动叠加，质点的位移矢量表成振型坐标的组合：

式中：[φ]为振型矩阵；｛φ｝j为第j阶振型列矢量，｛q（t）｝= [q1（t），q2（t），…，qn（t）]T，qj（t）称为振型坐标，也称广义坐标。对于第i质点，由于第j阶振型在i自由度方向引起的位移记为uij（t），依据上述关系式可得到：

qj（t）振型坐标由式（5-117）可表示为

式中

将式（5-142）和式（5-143）代入式（5-141），则有

将式（5-144）代入式（5-139）得到

引入位移反应谱比值：

式（5-145）可改写为

荷载求出后，再求各阶振型的响应，与前述用加速度反应谱求荷载方法相同。

3）速度反应谱求算地震动荷载。把各阶振型振子的振动看成单质点系，建立三种反应谱之间的关系，忽略阻尼的影响，根据能量守恒原理，应有

式中：umax为地震动最大位移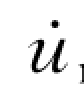；max为最大振动速度。

或写成

式中：Δ为最大位移；V 为振速最大值。

另一方面，单质点体系在地面运动震动加速度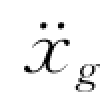（t）作用下有

也可写成

只取最大值，则

由式（5-151）可知

位移谱

速度谱

加速度谱

三种反应谱存在以下关系：

严格地说Sa应称为拟加速度反应谱，Sv称为拟速度反应谱，Sd称为相对位移反应谱。

根据这个单质点系的三种反应谱关系，直接推出多质系质点i第j阶振型引起的地震力，则有

或

由Sd和Sa二者关系得出的Sa近似性较好，而由Sd和Sv二者关系得出的Sv可能在低频时会产生较大误差，因此对于爆破地震这种高频（相对于通常的结构物频率）地面运动，要特别注意不宜直接用上述三联谱的关系，而应直接由杜哈姆积分求得，即

近似取ζj=0，则

而

而比较式（5-158）与式（5-159），显然有

而在ζj=0时，关系式（5-156）是成立的，因为

与式（5-159）相比较，可见

在分析研究爆破工程结构地震反应，按照反应谱理论计算地震作用时，不宜用式（5-155）和式（5-156）将加速度谱或位移谱换算速度谱值。