(1)平衡方程的建立。爆破地震或天然地震动地面加速度、速度、位移,无论用哪一个运动量,对地面的结构进行激励,必将引起结构振动。设单质点质量(m)—弹簧(k)系统支承在地面上,如图5-10所示,在地面产生的位移为xg(t),质点m产生振动,质点相对地面的位移为u(t),质点m产生的绝对位移则为
![]()

图5-10 地面位移激励单质点振动图示
相应的绝对加速度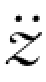 (t)、绝对速度
(t)、绝对速度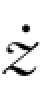 (t)应分别为
(t)应分别为

根据动力平衡条件,写出运动平衡方程如下:
![]()
移项后有
![]()
方程的右端项即为激励力f(t),是由地面运动速度与位移构成的,式中m、c、k依次为质量、阻尼和弹簧刚度。
无阻尼自由振动方程,当f(t)=0时,且c=0时,式(5-81)变为

这就是第5.1节所述单质点体系的有阻尼自由振动方程。
(2)爆破地震动位移和速度激励单质点弹簧体系动力反应解。自由振动的方程与本章5.1.2节所述完全相同,其解答也一样,这里就不再赘述。
将方程式(5-81)变成标准形式,即用质量m除方程式(5-81)各项,则可写成:
![]()
式中
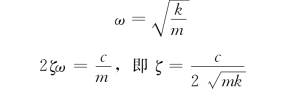


又可写为
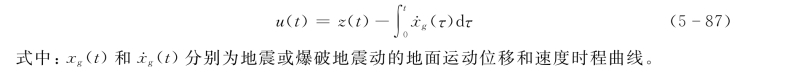
通常在计算结构内力即动应力、应变等参数时,应采用结构相对位移,式(5-87)完整的表示应为
![]() (https://www.daowen.com)
(https://www.daowen.com)
(3)爆破地震动速度和位移激励单质点系动力反应的反应谱法。在第5.1节已经介绍了由加速度激励求解的反应谱方法。众所周知,直接用爆破地震动速度、位移时程曲线输入式(5-88),用数值积分法求出其位移反应,问题同样可以解决,但通常计算爆破地震动作用时,只需求出最大反应,即最大位移时的作用荷载,再求出相应的内力反应,因此并不需要求振动响应的全过程。
假设式(5-88)的最大值为Δd,它应等于:

设单质点位移动力放大系数为βΔ,即
![]()
|xg(t)|max表示位移xg(t)的最大绝对振幅值。
地震动作用在质点上的惯性力等于质点质量乘以绝对加速度(取最大值),即
![]()
在不计阻尼力时,这个惯性力应等于单质点系的弹性抗力,弹性抗力为
![]()
k为弹簧刚度,且有k=mω2,同时用Δd表示相对位移的最大绝对值,式(5-93)变成:
![]()
由式(5-91)知Δd=βΔ|xg(t)|max,地震惯性力用地面运动位移表示,则为
![]()
前面已讲过阻尼为零时FI=Fs,并用F表示,故单质点系受到的地震动作用为
![]()
式中βΔ 可用位移反应谱确定。
在爆破地震动研究中,往往习惯采用振动速度作为控制标准。现推求以地面运动速度表示的作用荷载计算公式。为此,将式(5-88)对时间τ微分一次,可得相对振速为
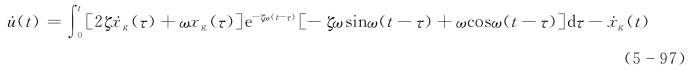
地震动在单质点上的作用力等于弹性抗力,于是有
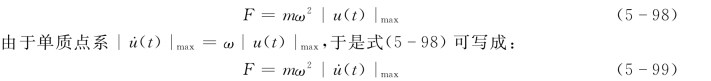
如果引入速度表示的单质点系动力放大系数βv,则式(5-99)可表示为
![]()
βv是以速度表示的动力放大系数,可用速度反应谱曲线确定,|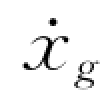 (t)|max为爆破地震地面运动的速度绝对值的最大值。
(t)|max为爆破地震地面运动的速度绝对值的最大值。
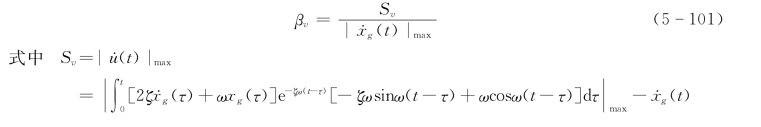
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





