（1）多质点系的振动微分方程。图5-7为多质点系结构等效体系，ui（t）表示质点i的相对位移，ug（t）表示地面运动位移。受爆破地震动作用时，多质点体系的每一个质点受到三种力：弹性恢复力（或抗力）、阻尼力和惯性力。

作用在质点i上的弹性抗力为

图5-7　多质点结构等效体系

阻尼力为

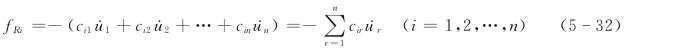
上两式中：为质点相对速度；kir表示在第r质点产生单位位移，其余质点不动的情况下，在第i质点上产生的弹性抗力；cir表示在第r质点产生单位速度，其余质点速度为零的情况下，在第i质点上产生的阻尼力。

惯性力为

式中：üi为质点相对加速度；üg为爆破地震动加速度。

根据牛顿第二定律，多质点系弹性运动平衡方程为

即

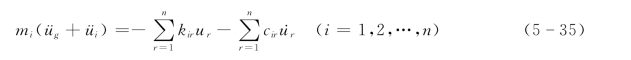
或

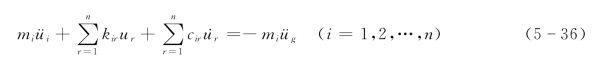
式（5-36）为多质点系在爆破地震动作用下的运动方程组，有n个质点，就有n个方程，写成矩阵形式更直观，如下：

通常把刚度矩阵简写成黑体字母[K]，阻尼矩阵简写成[C]，质量矩阵简写成[M]，于是有：

对于有三个质点的弹性体系 （见图5-8），质点1、2、3的质量为m1、m2、m3，相应的弹性刚度为k1，k2，k3，阻尼为c1，c2，c3，现写出质量矩阵、刚度矩阵与阻尼矩阵如下：

图5-8　三质点弹性体系

在实际工程中，有些工程可简化为单质点体系，但绝大多数的工程，均可简化为多质点体系进行计算，如电视塔架、水工上的重力坝、塔柱、塔架等，多层框架的房屋，可按层设为质点，把结构重量分布在各层上，各层之间的柱形成为弹性支撑杆，质点由支撑杆支承，形成弹簧，这样，整个多层框架的振动体系就由多质点体系所等效；又如高耸的烟囱，按高度等间距分成若干段，每一段分界线的标高处设置为质点，把每一段的1/2的重量堆置在该段的上、下的分段线标高处，即形成了质点，每一段的抗弯或抗剪刚度按该段的断面尺寸大小和材料弹性常数可以算出，这样也形成了多质点体系，用这个体系等效于实际的烟囱结构的振动体系，除此以外，还有高层工民建结构、电视塔架、水工上的重力坝、塔柱、塔架等，都可简化为多质点体系进行计算。

在水工结构上，像重力坝，也可类似于计算烟囱的方法，形成多质点的弹性振动体系，来研究它的爆破地震动反应。假设将某重力坝沿高度分成10段，每一段的分界线作质点标高位置，形成10个质点，如第6个质点质量为m6，它由第6段质量的1/2加上第7段质量的1/2组成，这就构成了该质点。坝顶部的质点质量m10就只取第10段质量的1/2。各质点间的刚度系数ki由各段的断面尺寸及材料性质等确定。这样就形成了重力坝弹性水平振动的多质点等效体系（见图5-9）。由于重力坝断面是变截面，水平振动是弯剪联合作用，因此计算断面刚度时应同时考虑弯剪效应。

（2）多质点系的振动方程及其解。

1）阻尼矩阵的建立。为了便于求解运动的微分方程组，假定体系有两组阻尼器，其中一组与质点质量相连，阻尼力与质量相关，另一组与弹性支撑相连，阻尼力与弹簧刚度相关。分别用两个比例系数α1及α2表示质量与刚度对阻尼力大小的贡献。如果给出了α1及α2，阻尼矩阵[C]就可按式（5-40）建立：

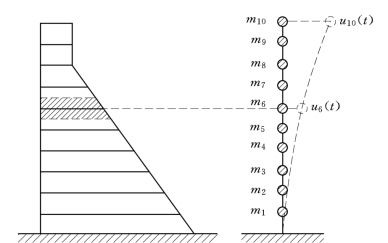
图5-9　重力坝的多质点系弹性振动体系

现在讨论α1及α2的确定方法。按上述假定，对多质点体系的质点i建立运动方程为

将式（5-40）代入式（5-41）后，变成：

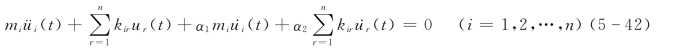
对于任何阶振型，各质点在任一时刻的位移都保持比例不变，也就是说弹性质点体系各质点的变位所构成的形状在任何时刻都是几何相似的。因此，对n阶振型，位移可做如下变换：

式中：φin、φrn分别为振型位移振幅。

将式（5-43）代入式（5-42）得到：

令

n阶振型的临界阻尼力系数可写成(www.daowen.com)

n阶振型阻尼比为

由式（5-47）解出有α1及α2：

给出任意两个振型的自振频率ωi、ωj和相应的阻尼比ζi、ζj，并代入式（5-48），得到关于α1及α2的二元一次代数方程：

用消去法解出α1及α2有：

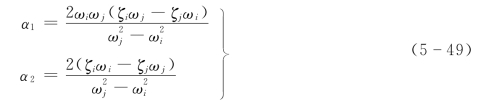
式中：ωi、ωj分别为任意第i阶和第j阶频率，比如说第1阶和第2阶，对具体的结构，可用计算方法或试验方法确定；ζi、ζj分别为第i阶和第j阶阻尼比，由试验确定。

通常各阶振动的阻尼比相差很小，特别是前n阶阻尼比几乎是相同的，即取ζi=ζj=ξ，因此由式（5-49）可得：

ζ和ω均可取结构的第1阶频率和相应的阻尼比，即ωi=ωj=ω，式（5-50）可进一步简化为

按照上述方法计算出系数α1及α2后，阻尼矩阵就可按式（5-40）建立起来，这时多质点系爆破地震的振动微分方程式（5-36）则改变为

写成矩阵形式为

经上述变换后，阻尼矩阵就由质量矩阵与刚度矩阵线性组合而成，这样处理后求解方程式（5-36）就变成求解方程式（5-53）。

2）振型分解法求解。将方程式（5-52）中的质点位移，按主振型展开，得

相应的质点速度、加速度可由式（5-54）对t求一阶及二阶导数得

将式（5-54）～式（5-56）三式代入式（5-52），有

对于不计阻尼的多质点自由振动方程组的解

将式（5-59）代入式（5-57），并经整理后得

将式（5-60）等号两边分别乘以振型位移uik，并对i求和，利用振型正交性，整理后可得出

式中

rj称为振型参与系数。

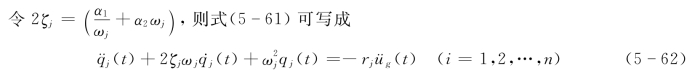
至此，已将原多质点系振动微分方程组分解成n个以振型坐标qj（t）表示出的独立微分方程（j=1，2，…，n）。这些微分方程是互相不耦联的，可以独立求解。每一个振型都有一个独立微分方程，只是方程中的频率ω和阻尼比ζ为相应那一阶的ωj及ζj值。这样的每一个方程与单质点系的爆破地震作用的振动微分方程是相同的，仅仅是右端项里增加了一个振型参与系数rj，每一阶的振型参与系数rj是不一样，按上述公式可以计算出来，因此方程式（5-62）的解仍可按单质点系相同的方法求解。求解的结果为

或写为

式中

Δj（t）相当于频率为ωj、阻尼比为ζj的单质点体系在爆破地震动üg（t）作用下的位移。把各阶振型的主坐标qj（t）（j=1，2，…，n）都求出后，多自由度体系的爆破地震动反应，即可用主坐标加以组合而成，通常称为振型叠加。由于天然地震动频率低，往往只需求出前n阶的主坐标就可以较真实地反映出结构的动态响应了，但对于爆破地震动，由于其振动频率较高，最大反应在10Hz以上，因此计算的振型阶数不能太少，究竟取多少阶，要由具体结构物频率谱及地震动的频率来确定。

原几何坐标系的质点位移，可将上述求出的主坐标代入式（5-54）得到为