（1）单质点系地震动力平衡方程。为了说明如何用反应谱方法计算结构动力反应，先对单质点系进行讨论，即质量—弹簧体系（见图5-1）地震动作用下的动力平衡方程。

设单质点质量为m，它的弹性支撑刚度为k，阻尼为c，随时间变化的外作用荷载为f（t），根据动力平衡条件，动力平衡方程可表述为）

式中：ü（t）、u·（t）、u（t）分别为单质点体系的振动加速度、速度和位移。

受爆破地震动作用时，f（t）应为地面运动加速度üg（t）产生的惯性力，即

在忽略阻尼的情况下，单质点弹簧体系的自振圆频率为

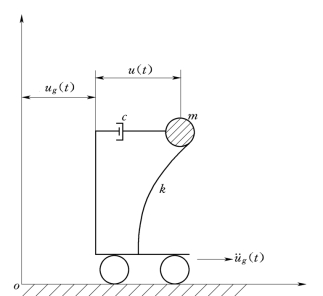
图5-1　单质点弹性体系

无阻尼时的频率值与有阻尼时的频率值很接近，一般情况下，不特别说明，频率就取式（5-3）的值。

把式（5-2）、式（5-3）代入式（5-1），加以整理可得到标准的爆破地震地面运动作用时的单质点系振动方程，为

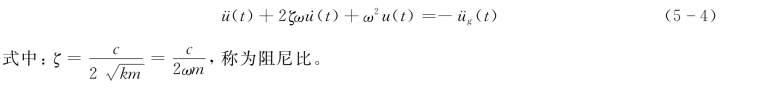
这就是单质点系爆破地震作用的动力平衡方程。

（2）单质点弹性体系动力平衡方程的解。

1）自由振动的解。

求单质点系的爆破地震反应，就是求解方程式（5-4）。由结构动力学知，对没有受外力作用体系的自由振动方程，式（5-4）右端项为零，即

按常系数线性微分方程的解法，可假定有下列形式的解：

式中：h为待定常数；t为时间变量；e为自然对数底。

将式（5-6）代入式（5-5），可得

这是一个二次代数方程，称为特征方程，它的解应有两个根。

现在来讨论不同阻尼情况下的自由振动的解。

当ζ=0时，即无阻尼情况，特征方程的两个根为

显然式（5-5）的通解为

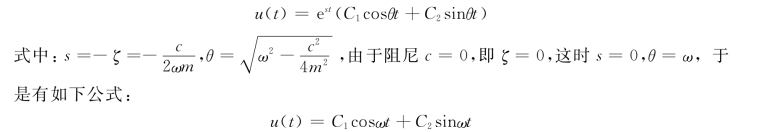
根据初始条件，即

当t=0时

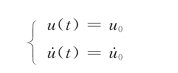
确定常数C1及C2，得

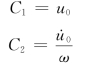
于是无阻尼单质点系的自由振动解为

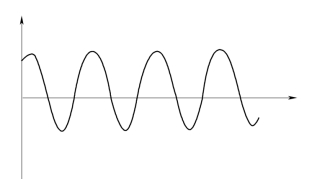
它的振动曲线 （见图5-2）表明，是振幅无衰减的谐振。

当0＜ζ＜1时，方程式（5-7）的两个根为

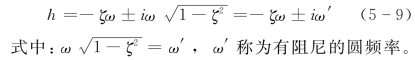
因为是两个复根，故自由振动方程式 （5-5）的一般解为

(www.daowen.com)

图5-2　无阻尼等幅谐振

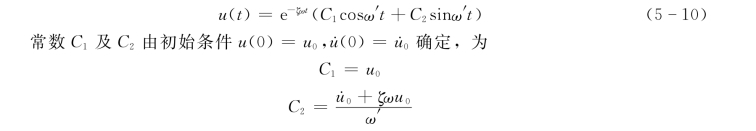
代入式（5-10），即得单自由度体系有阻尼自由振动的一般解为：

经变换可写成式（5-12）：

式中

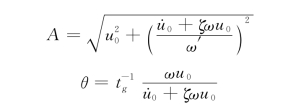
单自由度体系有阻尼自由振动的曲线见图5-3，此振动为谐振的衰减振动，振幅最后衰减到零，振动停止。振动周期不变为

当阻尼较大时，常称为过阻尼，这时阻尼比ζ ＞1。而当ζ=1时称为临界阻尼，这时特征根为

这时，式（5-8）中根号内的值等于零，就是临界阻尼的条件。这意味着方程不含振荡项，只有振幅的衰减。根据微分方程的理论，齐次微分方程有重根时，其通解为

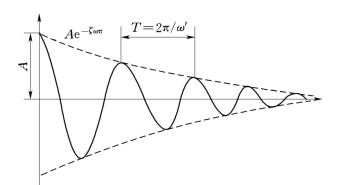
图5-3　小阻尼自由振动衰减

由初始条件可确定出常数C1及C2，式（5-13）可写成

这表明，临界阻尼时的自振响应，只是振幅逐渐衰减到原位，不产生往复振动。临界阻尼值是不出现质点往复振荡的最小阻尼，当阻尼大于此值时，也同样不产生往复振荡，其振幅衰减曲线如图5-4所示。

图5-4　临界阻尼自振响应

爆破地震作用单质点系的自由振动反应，就可以从上述自由振动解出发来求解。

按照式（5-11），当初位移为零时，仅在初始速度u·0的影响下，自由振动解为

2）爆破地震动激励强迫振动的解。爆破地震地面运动加速度üg（t）激发的单质点系的振动平衡方程式（5-4）的解由两部分组成：第一部分为初始条件引起的自由振动，解的结果为式（5-11）；第二部分则为地震动加速度üg（t）强迫其振动的结果。加速度üg（t）通常不能用解析式表达，可用离散的üg（ti）～ti（i=1，2，…，n）表示，它的时程曲线如图5-5所示。

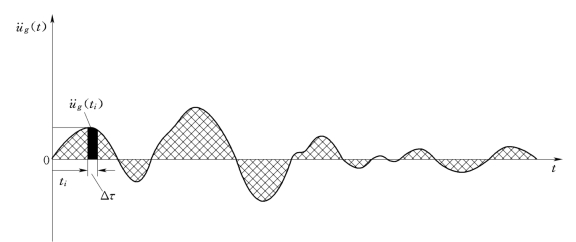
图5-5　爆破地震动加速度时程曲线

对于加速度时程曲线，每一个离散的小条形面积为振动速度增量都可用式 （5-16）表示，因此震动连续作用的总位移，可对Δu（ti）求和得到，即

当Δti→0时，取极限，每一个起始坐标用τ表示，则式 （5-17）右端变成积分表示：

如果计入阻尼对频率ω的影响，则式（5-18）变成：

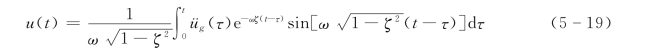
假设阻尼为零，式 （5-19）简化为

以上求得了爆破地震动单自由度结构强迫振动的解，它和初始扰动产生的自由振动解相加，就构成单质点系在任何初始条件下受爆破地震动作用的完全解。通常认为，在天然地震作用下，由于自由振动部分在阻尼作用下，很快衰减了，可以忽略，因此只取式（5-18）或式（5-11）的解作为其振动响应的解，但是，对于爆破地震，由于其作用时间短，强迫振动部分也是短暂的，是否能够将初始扰动部分忽略，还应慎重。

3）冲击荷载强迫振动的解。

方程式（5-1）右端项f（t）如果是冲击荷载P（t），则可以根据地震惯性力的方法，单质点位移反应可以表示为

对无阻尼的单质点体系：ζ=0，ω=ωd，式（5-21）可变为