爆破地震动常用地震动速度来评价其震动强烈程度，通常记录的是地震动的加速度或速度时程曲线，但用地震动速度记录来求算反应谱，更加合适。这就需要建立以速度位移激励作用的结构动力平衡方程。对于求解反应谱，只需要单自由度运动方程即可。作者曾在文献[4]中建立了这一方程，也可见本书第7章。这里直接引出单质点系的速度位移激励的强迫振动方程及其解答式。

运动方程标准化形式为

方程式（4-22）的解可用杜哈姆积分表示如下：

式中

如果知道地面振动速度x.g（t），积分一次可以得出位移xg（t），于是式 （4-23）可表示为

因为式（4-24）求的位移是绝对位移，其相对位移应为

将式（4-24）代入式（4-25），且近似取ωd=ω，并用ω表示，于是有

根据式（4-26），可分别求出地震动的相对位移谱、相对加速度谱。

（1）相对位移谱。式 （4-26）右端的最大值，就是相对位移谱，用Sd表示，则为

显然当ζ=0时，相对位移谱Sd为

（2）相对速度谱。式 （4-26）对t求微分一次，可得单质点相对速度为

式 （4-28）的绝对最大幅值，即为相对速度谱值，用Sv表示，为

当ζ=0时，相对速度谱为

比较式（4-27）和式（4-29），显然Sv并不等于ωSd，Sv是cos的积分，而Sd是sin的积分。

（3）绝对加速度反应谱。由式（4-22）可知

将式（4-26）和式（4-28）代入式（4-25），则有

绝对加速度反应谱就是式（4-20）右端项的绝对值的最大值，用Sa表示，为(www.daowen.com)

当阻尼比ζ=0时，绝对加速度谱为

将式（4-27）与式（4-32）进行对比，可见，当阻尼比ζ=0时，有

式 （4-27）、式 （4-29）和式 （4-32）的结果表明，在ζ=0时，Sa=ω2Sd，但Sv≠ωSd。这与前述以地震动加速度激励的动力平衡方程求反应谱所表述的结果是相同的。

要求得反应谱的结果，还需借助数值积分来计算相应的杜哈姆积分，仍采用Wilson—θ法，假定在加速度线性变化的情况下，方程变换为

对于单自由度有

其中

将上述各值代入式（4-33），可求出Zt+τ的结果为

此式与式（4-16）基本相同，不同的是地面加速度换成了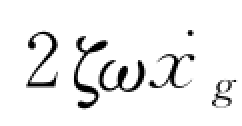（t+τ）+ω2xg（t+τ），其中的系数a1，a2，a3等也完全相同。为保证数值计算的无条件稳定，仍采用Wilson—θ法，即τ=θΔt，θ≥1.37，实际计算时取为1.40即可。

求解问题的初始条件，在t=0时刻，速度位移为零，即

将此结果代入方程式（4-22），则t=0时，有

这就是本问题的初始条件。

至此，求解问题已完全解决，根据所导出数学关系式编制程序，很容易在计算机上实现。

这里，需要强调一点的是，由于本方法所导出的平衡方程，采用的是绝对位移、绝对速度与绝对加速度，而反应谱常采用比值谱表示，应为

绝对加速度比值反应谱：

相对速度比值反应谱：

相对位移比值反应谱：