如前所述，现场直接测定反应谱的方法早已被淘汰。如果要获得比较准确的反应谱曲线，现在普遍采用强震（加速度）记录地面运动的加速度时程曲线，通过数值积分方法求解运动平衡方程式（4-1），其特解的形式一般是式（4-2），这就是大家熟知的杜哈姆积分。天然地震常采用地震动加速度来表示振动强度，地震动记录也是加速度时程曲线。

按照反应谱的定义，对天然地震而言，求地震动反应谱，就是求解以实际地震动加速度激励的动力平衡方程式（4-1）的解。获得准确的实际记录的加速度时程曲线，是求得可靠结果的前提。它要求测试记录系统有较宽的频谱特性，其频带可以覆盖地震动可能出现的频率。

按照式（4-1）的解，先求出相对位移谱，再按照式 （4-10）的关系推求拟速度谱PSv和拟加速度谱PSa，可近似取加速度谱Sa为PSa，即Sa≈PSa；近似取速度谱Sv为PSv，即Sv≈PSv，并可绘出三联对数坐标反应谱。

对爆破地震，通常震动频率较高，然而对环境影响效应，低频影响应是至关重要的。因此不能忽视低频成分记录的真实性，但往往容易被疏漏。这一点应引起足够的重视。

计算反应谱，实际上就是求解地震动加速度激励下单自由度体系的反应。单自由度运动方程是

式中：m、c和k分别为单质点的质量、振动阻尼和支承的刚度。在单质点情形下，可设c=2αm，α=ζω。

ζ为阻尼比，为单自由度体系的圆频率。在线弹性振动时，c和k均不依赖于位移u，是常量。

按上述假定，方程式（4-11）可改写为式 （4-1）的形式，将任何地震动加速度记录（爆破地震动记录也一样）经数字仪处理后，代入其右端，就可逐步求解。这个方法的独立参数只有阻尼比ζ和体系的圆频率ω两个量。ζ与结构的类型及材料性质有关，一般工民建结构，常取ξ=0.05。给定一系列的圆频率ω就可计算每一个ω下的最大响应值，形成的一个序列ωi～Si（i=1，2，…，n），这就是工程反应谱。

方程求解采用Wilson—θ法。

初始条件为

在位移、速度初始条件给定的情况下，代入方程式 （4-1），可求出相对加速度的初值为

（0）由地震动加速度记录确定。

天然地震情形下，一般结构物的基本周期（T=2π/ω）均在0.05～3.0s之间，一些高柔结构物的周期可能要长一些。但对爆破地震动，特别是大多数的工程作业爆破情形，结构物的周期相比来说要短一些。在计算反应谱选取ω时，应注意这一点，以免漏掉反应谱峰值。

关于求解的Wilson—θ数值积分方法算式的推导将在第5章中详细介绍，这里只引用其结果。Wilson—θ法，实质上是线性加速度法的一个改进，它改进为无条件稳定的方法。方程变换后为（对单质点系，不用矩阵形式）

(www.daowen.com)

将式（4-14）和式（4-15）代入式（4-13）中，整理后得

式中

θ为Wilson常数，θ≥1，Δt为时间步长。Wilson指出，当θ≥1.37时，计算是无条件确定的。

式 （4-16）计算得到ut+τ之后，可按线性加速度假设，计算t+Δt时刻的结果为

至此，计算反应谱的全部公式为式（4-16）、式 （4-17）、式 （4-18）、式 （4-19）以及初始条件式（4-12）。

这里需要注意的是，解方程式 （4-13）需要列出右端有效荷载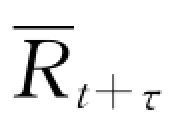，它是t+τ时刻的地震动加速度值乘以质点质量，即

图4-7　加速度反应谱曲线

它的第一步取t+τ，随后每步增加一个Δt，即t+τ，t+Δt+τ，t+2Δt+τ…，即除第一步外，每步都是间隔Δt，而不是每一步按τ间隔取值。

加速度反应谱曲线如图4-7所示。