地震动反应谱曲线理论是在20世纪30年代有关工程地震与地震工程的科学家研究天然地震作用时，在研究工程结构物动力反应中所建立起来的一种理论。这一理论已广泛应用于地震工程结构的抗震计算与抗震设计中，并为各国抗震设计规范所采用。

就反应谱而言，它是描述地震动频谱组成的一种形式。其最有意义的一面是直接反映地面运动，反应谱建立了地面运动频谱与工程结构物固有频率的密切关系，以最简单的方法反映了与工程设计最有直接关系的地震地面运动频谱特性。

下面用图解形式来说明反应谱的基本概念，图4-1显示了地面运动 （输入）和结构响应（输出）的时程与反应谱的关系。

图4-1　反应谱图解说明

（a）地面运动时程 （地震波）；（b）单自由度振子；（c）振子反应时程线；（d）反应谱

反应谱图解形象地说明了不同频率单自由度系统的结构物（振子）在爆破地震地面运动的作用下（输入）各振子产生的振动反应 （输出），用振动速度时程曲线表示，每一个振子（频率不同）的时程反应的单边最大振幅值（绝对值）所连成的曲线，就是反应谱曲线。反应谱曲线的谱值与阻尼有关，给定一个阻尼，即可得到一条曲线。零阻尼的谱值最高，随着阻尼的增大，谱值减小。大多数工程结构物，通常阻尼比取为0.05，但如果使阻尼比值更加准确，最好的方法还是通过实测确定。

用数学公式定义反应谱，可根据图解的概念（见图4-2），假定单自由度体系的质点m对于地面的相对位移为u（t），而相对固定坐标系绝对位移为u（t）+ug（t），相对于固定坐标的地面运动加速度为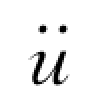（t）+ （t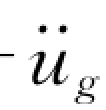），于是该质量的弹性振动的运动方程可表示为

图4-2　单自由度体系地面运动作用简图

式 （4-2）是式（4-1）解的一个一般公式，对于任何一个自振频率为ω、临界阻尼比为ζ的单质点体系，在给定的地震地面运动加速度（t）作用下的位移反应都可以计算出来。这个反应也是时间t的函数。虽然有了一般解答式 （4-2），但由于地震地面运动加速度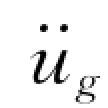（t）是不规则的任意函数，不能用精确的数学解析式来表示，所以通常都是用数值积分方法来求解。随着现代计算技术的不断发展，通过编写计算机程序，可以很容易得到所需要的结果。

现通过举例来说明这一计算结果。对于给定的三个不同周期的单质点系，在TAFT地震动加速度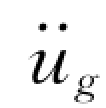u（t）的作用下，按式（4-2）计算出其加速度反应[5]时程线，如图4-3所示。由图4-3可见，不同单自由度（T或ω不同）在相同地震动加速度的作用下，引起的反应的时间过程、峰值和频率都不相同。

在评价结构振动安全度时，每一个反应时间过程中所产生的最大反应值是最备受关注的。对于相对位移反应，u（t）的最大反应值就是u（t）max（用Δ表示），这个值可以由位移反应时间函数（或过程）得出。给定阻尼比ζ，对于不同的自振频率ω，都可以求出其相应的最大位移u（t）max。这样，相对位移最大反应就可看作自振周期T （或频率）的函数。每一条地震动记录（t），都可以计算出一系列不同自振周期（Ti）的单质点系的位移反应（Δi）。

Δi～Ti（i=1，2，…，n）的关系曲线就是相对位移反应谱曲线，即以位移Δ为纵坐标，自振周期T 为横坐标的曲线。图4-4绘出的是两条地震记录的相对位移反应谱曲线[5]。

以上讨论了相对位移反应谱曲线，对于单质点弹性体系，如果知道了它的相对位移最大反应值，其相应的应力状态就可以计算出来。据此，可对结构进行抗震设计或抗震安全评价。这时，仅有相对位移反应谱就显得不够用，还需要相对速度反应谱和绝对加速度反应谱，并建立这些反应谱之间的相互关系。

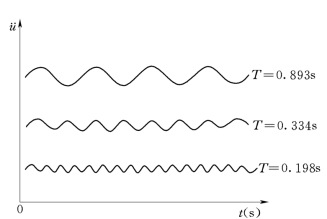
图4-3　加速度反应时程线

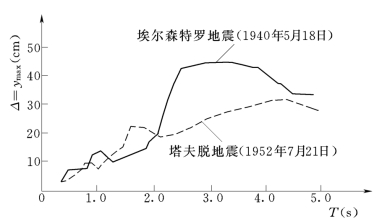
图4-4　相对位移反应谱曲线

按以上所述，标准反应谱定义如下：

（1）相对位移反应谱。相对位移反应谱就是取式（4-2）右端积分的最大值，用符号Sd表示，有

当ζ=0时

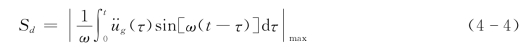
（2）相对速度反应谱。相对速度反应谱即将式（4-2）对时间t求导数，可得到相对速度解为

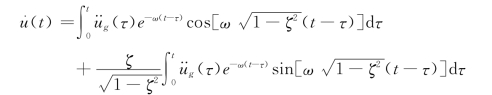
其相对速度反应谱，即|u.（t）|max，用符号Sv表示，有(www.daowen.com)

当ζ=0时

（3）绝对加速度反应谱。绝对加速度等于相对加速度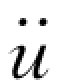（t）与地面运动加速度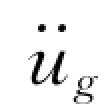（t）之和。由式（4-1）应有

将式（4-3）及式（4-5）代入上式右端，绝对加速度反应谱值用Sa表示，有

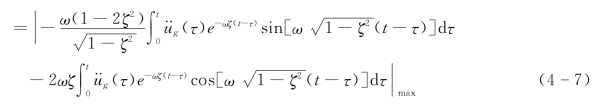
当ζ=0时，

对式（4-4）与式（4-8）进行分析，可得出如下结果：

由以上推导结果可见：三种反应谱的谱值并没有一个简单的换算关系，只有在阻尼比为零的情况，即当ζ=0时，绝对加速度谱值等于相对位移谱值乘以圆频率的平方，即

而相对速度谱值不能建立与相对位移谱值的简单关系，即使在阻尼比ζ=0时也是如此。但对于天然地震，在大多数频率范围及阻尼范围内，振幅、相位都是时间的慢变函数，近似认为相对速度反应谱值等于相对位移反应谱值乘以圆频率，即

这种相互关系是近似的，为了区分式（4-5）及式（4-7）建立的标准反应谱和由式（4-9）建立的近似相对速度谱与绝对加速度谱，特别把式 （4-9）得出的速度谱与加速度叫做拟速度反应谱和拟加速度反应谱，并分别用PSv和PSa两个符号表示，以示区别，即

PSv与Sv的近似性比PSa与Sa的近似性差，即使在ζ=0的情况下，PSv也不等于Sv。这是很显然的，因为ωSd的积分中包含的是sin （正弦），而Sv的积分中包含的是cos（余弦）。

PSv与Sv的差异，还应注意的是，对长周期的柔性结构物，这种柔性是相对而言的，即地运动周期相对结构周期短得多时，就可认为是柔性了。这时，如果地面运动频率很高，柔性结构刚度相对很小，质量体的相对位移也很小，几乎无放大，这时质量体与地面间的相对位移几乎接近于零，结构体的位移就是地面运动的位移。因此当周期T 很大，即当T→∞时，其反应谱值应取如下结果：Sd→地面位移峰值；Sv→地面速度峰值；Sa→0。

但是，在与上述相同的情况下，拟加速度谱值会相当小，即当T→∞时，因为Sd是一个有限量，故有

图4-5　三联反应谱

（4）三联地震反应谱。根据式（4-9）的关系，用对数坐标把位移、速度和加速度反应谱绘在同一张图上，通常称为三联坐标地震反应谱（简称三联反应谱）。在三联反应谱图中，如图4-5所示，速度谱就是指PSv，加速度谱就是指PSa；而标准反应谱中，相对速度谱就是真正的最大相对反应速度Sv，绝对加速谱值就是真正的最大加速度Sa。

三联反应谱图中，位移、速度、加速度反应谱存在的下列关系：

如果把PSv近似为Sv，把PSa近似为Sa，这种近似，对于天然地震那样的振动，通常是可以接受的，因为地震动频率、阻尼与大多数工程结构频率及阻尼比较接近；但是对于长周期结构，即当结构频率比地震动频率低很多时，直接致PSa=Sa，PSv=Sv，可能有较大误差，特别是速度谱的误差很大。这里要特别指出，对于爆破地震，如果采用反应谱理论计算结构的动力响应，即采用PSv代替Sv时会引起较大误差，这是因为爆破地震往往都是用振动速度来衡量地震动的，可见研究爆破地震作用的结构物动力响应，采用三联反应谱时，应该审慎。

关于阻尼对各反应谱之间关系的影响，由式 （4-8）可知，当阻尼比ζ=0时，PSa=Sa，但由式（4-6）可见，对于阻尼比ζ=0时，PSv≠Sv。这一结果很重要，它说明，用速度反应谱计算结构的爆破地震响应，应采用由爆破地震动速度记录直接求出的速度反应谱曲线较合适。

以上所述可知，应用反应谱理论研究结构爆破地震响应时，建立适合爆破地震的地面运动反应谱是非常重要的。