拱坝是一种复杂的三维结构，拱和梁的联合作用，承受巨大的水荷载。为分析它的动力反应，目前，拱梁分载法（亦称试载法）和有限元方法是通常采用的两种主要方法，它们的力学模型现分述如下。

（1）拱梁分载法力学模型。拱梁分载法，基本概念明确，经过长期实际工程的检验，计算成果可靠。拱坝设计规范也一直明确规定拱坝的应力分析均以拱、梁分载法计算成果作为评价安全的标准。图3-7为试载法拱梁结构单元，k为梁j与拱i的交点。

（2）三维有限元模型。有限元法，可以模拟坝体孔口及复杂地基的情况，用它计算的频率、振型、变位都较准确，惟有应力在转角部位，近基础部位产生较严重的应力集中，网格对应力影响特别大。因此剖分网格时有一定经验性。拱坝有限元网格图如图3-8所示。

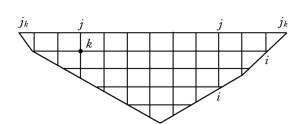
图3-7　试载法拱、 梁图

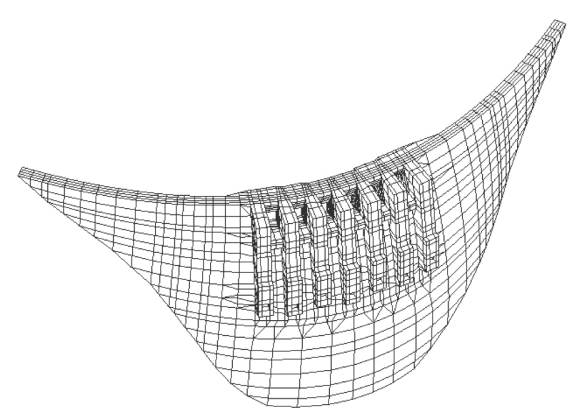
图3-8　拱坝有限元网格图

试载法是以梁上或拱上分配的径、切、扭荷载为方程的未知量，在各种荷载时，按拱、梁支点处径、切、扭变位一致条件建立联合方程组。

动力分析，常采用柔度矩阵来表示拱坝结构的运动方程，来求解特征值及特征向量，动力响应则用反应谱方法求解。

由拱梁交点变位相容条件可得

式中：∑表示对拱上的或梁上所有的点求和；i、i′、j、j′、jk、j′k表示拱、梁号；｛Pe｝表示梁的荷载列向量；｛PA｝表示拱上的荷载向量；[CkL]梁或拱 （L可取梁或拱号j或i）上所有交点分别作用单位荷载在k点引起的变位方阵。(www.daowen.com)

对每一个拱、梁交点均可列出一个位移相容方程，以矩阵表示为

解出｛Pc｝为

式中：ρ为水体密度，g=9.81m/s2；y为计算点至水面深度，m；h为计算截面水深度，m。

柔度法求解则其特征方程为

[I]为单位阵；[δ]为柔度矩阵：[δ]= [C]｛[A]+[C]｝-1[A]

[M]质量矩阵；[Y]特征向量。为特征值，一般用λ表示。

由式（3-63）用迭代法求出各特征值特征向量后，即求出各阶频率及振型后，再用反应谱法计算动力反应。

试载法的动力分析，能较好地计算拱坝应力，并能合理地解决动静应力叠加，为评价拱坝动力安全性提供了较准确的结果。