将实际无限关系结构体系离散为有限个单元的近似结构体系，这种近似结构体系变形与力的关系是整体刚度矩阵来考虑的，而整体刚度矩阵是由各单元体的刚度矩阵集合而成的，通过力学分析，建立单元体节点的位移与相应节点力之间的关系，即可求出单元刚度矩阵。

设离散的结构体系受自重与外力作用，每个单元也由于力的作用产生位移和应力。以三角形平面单元为例、设其中一个单元为ijm，单位厚度为t，在i节上，节点荷载为

把作用在i上的水平节点荷载用单元边界上分布力代替，相应的竖直荷载也用单元边界上的竖直分布力代替，如i点的节点力Ui及Vi是ij边界与mi边界分布力的水平合力和竖直合力[见图3-3 （b）]。

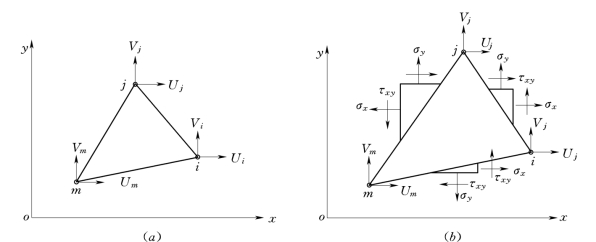
图3-3　单元节点荷载及应力

（a）节点荷载；（b）单元应力

节点j和m 的节点荷载Ui、Vi、Um、Vm也可同样求得，于是单元i、j、m 的节点力合并起来，可表示为

利用矩阵[B]，即式（3-12），式 （3-23）可写成：

应力用节点位移表示如下：

式 （3-25）代入式（3-24），则有(www.daowen.com)

令

于是有

这就是单元节点荷载与单元节点位移之间的关系，矩阵[K]e称为单元刚度矩阵。

把矩阵[B]用分块形式表示，即有式（3-11），则刚度矩阵可写成分块形式：

上式中的[Krs]为2×2阶子矩阵。

对各向同性弹性体平面应力问题的[Krs]，将 [D]和 [B]表达式代入式 （3-30），可得到

对平面应变问题，式 （3-31）中E换成E/（1-μ2），μ换成μ/1-μ即为相应的子矩阵。

以上是通过直观的方法来建立单元刚度矩阵，这样做易于理解，力学概念比较清楚。但对比较复杂的单元，用这种方法就很难建立单元刚度矩阵，而应用能量原理进行单元分析建立有限单元法的基本公式则是一个好的方法，它克服了直观建立单元刚度矩阵方法的缺点，在数学理论上是严格的。关于这方面的详细论述，可参阅有关专著。