（1）平面单元。从单元形状看就是三角形单元和四边形单元两种。三角形单元又可分为三种不同结点的三角形单元。3节点的三角形单元内为常应变，精度差，6节点的三角形单元精度次之，9节点的三角形单元精度最高。四边形单元又可分为4节点、8节点、12节点的等参单元，其节点多，精度高，因此单元可以取得大些，即网格可以稀疏一些，即使这样，其精度仍会比一般四边形单元的高。

在实际工程计算中，如何选择单元类型，对提高精度是至关重要的。一般来说，常应变三角形单元和四边形单元，现在已很少被采用。这是因为工程结构中的应变和应力场是随着坐标位置变化而急剧变化的，应用这类单元，只有通过加大单元网格密度，才能达到所要求的精度，但单元密集，往往会造成节点过多，方程组太大的结果。因此实际工程中多采用高次的三角形单元或矩形单元，高次单元内部应力和应变是变化的，可以反映实际应力的变化情况，划分少量单元也可得到较高的计算精度。例如图3-1比较了用高次单元及常应变三角形单元的计算结果。图3-1 （b）采用常应变单元，在梁高度方向上布置了四排单元（五排节点），但精度值仅为理论值的86%，误差仍有14%，应力误差更大。采用高次的18个自由度的三角形单元，仅两个单元如图3-1 （c）所示，其挠度达到理论值的99.4%，误差仅0.6%，应力误差也仅2.3%，计算精度很高。

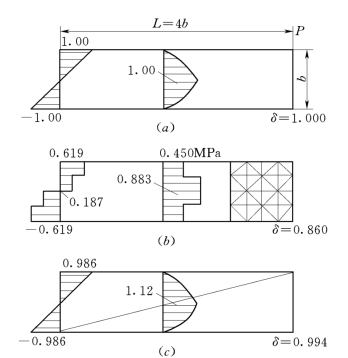
图3-1　悬臂梁， 常应变单元与高次单元比较

（a）梁理论；（b）常应变单元，128个单元，170个方程；（c）3节点18自由度单元，2个单元，24个方程 （引自文献 [4]）

对单薄结构，如隧洞衬砌，土中防渗墙厚度薄，不可能沿厚度方向划分出5排以上的单元，但单元少，误差大，因此应采用高次三角形单元或8节点等参单元。

（2）空间（三维）单元。空间（三维）单元可分为三种类型：四面体单元、六面体单元和等参数单元（表3-1）。

表3-1　空间单元类型(www.daowen.com)

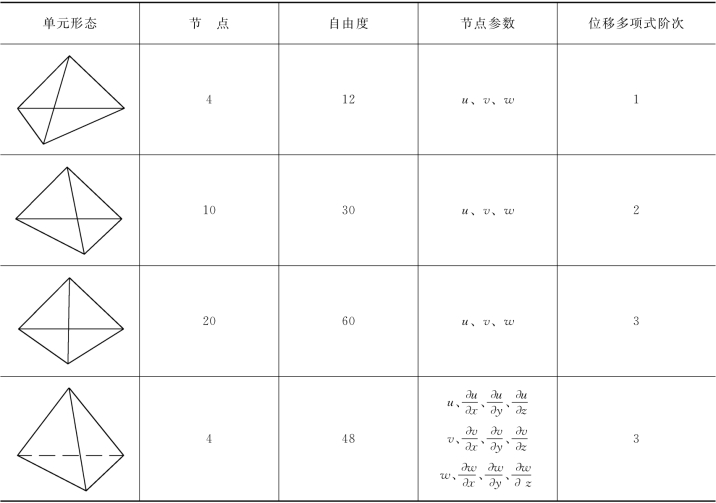
4节点12个自由度的四面体单元，能适应复杂结构的几何外形，单元内部应变是常量，要取得好的效果，必须加密网格，采用大量的单元。增加了节点的四面体，精度会提高。以48个自由度的四面体为例，每个节点采用12个参数。

六面体（8节点、24个自由度）单元形状规则，难以适应工程结构的外形，但可以和12个自由度的四面体联合使用，工程结构中，具有几何规则形状的使用六面体，不具有几何规则的部分则使用四面体。

等参数单元有较高的精度，也能适应复杂的边界形状，以20节点60个自由度的六面体单元和8节点24个自由度的棱柱体单元应用较多。

选择何类单元，不能一味增加自由度的数目和提高位移多项式的阶次，还必须注意原结构的特征和受力状况，如应力场变化急剧的地方，采用密集网格的四面体单元，是提高精度很有效的选择。

（3）弹性薄板单元或薄壳单元。在工程中广泛使用弹性薄板薄壳结构，在应用有限元法求解这类工程结构的弯曲问题时，可用离散的薄板单元代替原来的连续薄板结构，有限单元一般采用矩形板单元和3节点三角形单元，且3点三角形单元更能适应较复杂的边界。

有限元分析弹性薄壳结构，其方法有两种：一种是用板单元组成折板系统，近似代替原曲面薄壳结构；另一种则是采用曲面单元，由壳体理论推导单元刚度矩阵。

对于一些结构很单薄的薄壁结构，如压力钢管等，采用实体空间单元往往得出病态方程，采用薄壳单元则更合适。