土石坝的坝体是由强度低的散粒体堆筑而成的坝体，其体积大，坝的底部宽度比坝的高度大得多，坝体边坡平缓。它受库水作用不会产生弯曲变形，水平激励、水平向振动也不会产生弯曲，其变形是水平剪切变形，动力学模型也可用多质点剪切系模拟。

（1）多质点剪切系模型。模拟土石坝横截面的一维多质点振动类似于重力坝的作法，将坝体沿高度等分，形成质点质量，集合整个质点形成质量矩阵。

支承各质点刚度，按抗剪切作用计算各层刚度为

式中：Ki为第i层刚度；Gi为第i层土剪切模量；Ai为第i层截面面积；hi为该层的厚度，等于H/n，H 为坝高度，n为等分层数。

集合各层质点刚度，构成刚度矩阵，它是对称的三对角阵。忽略阻尼影响，可由建立的频率方程计算出各阶频率及相应的模态。利用反应谱法和时程法均可计算出地震动力反应。

（2）剪切梁模型。剪切梁模型适用于楼层的横梁、楼板等刚度比立柱的刚度大得多的楼房的地震反应计算，也适用于有限深度的均质土、砂、卵石地基的地震反应分析。结构物可等效为图2-6，坐标系为x （水平向），y （竖直向），设x向位移为u （x，t），竖向位移忽略不计。现取梁断面微元体bxdy，b为宽度 （常数），微元体底部作用剪切力为Q，顶部剪切力为Q+dQ，还有惯性力FI和阻尼力FD。(www.daowen.com)

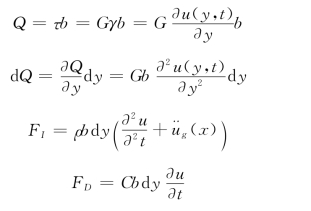
式中：τ为剪应力；G为剪切模量；γ为材料的容重；ρ为材料的质量密度；C为阻尼系数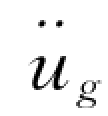，（t）为地面加速度。

由∑Fx=0可得剪切梁动力平衡方程：

引入阻尼比，式 （2-9）可写成：

方程用分离变量法求解，分离出一个贝塞尔方程，可计算出振型和频率；另一个为二阶非齐次方程，可求出地震反应。