这种力学模型，通常是取单位长度的坝块，把重力坝看成变截面竖直向悬臂结构。现在来介绍质点系的构成方法。沿重力坝高度方向等分n段，每段高度为H/n （H 为坝高，n为划分的段数），每一段的分界线作为质点质量堆积位置，内部分界线 （i）上质量等于界线上一段质量的一半和下一段质量的一半的总和，即

如图2-5所示。

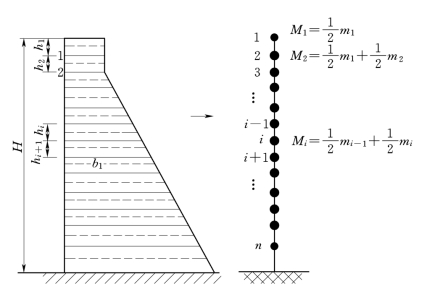
图2-5　重力坝多质点体系

mi为每一段的质量；Mi为每一质点的质量，堆积在每一段分界线上。于是质量矩阵为

对于标准的实体重力坝，则每一段hi的质量，可以用式（2-5）计算：

式中：bi为该段中线的长度，m；δ为坝块厚度（常取为单位厚度），m；γi为坝体混凝土材质容重，kN/m3；g为重力加速度，m/s2。(www.daowen.com)

相应于各质点的刚度：由于重力坝是变截面（梯形）悬壁式结构，底部断面为尺寸与坝高相当，它的水平变形由剪切和弯曲联合作用，其顺水流向的抗弯刚度为EIi，抗剪刚度为GAi/hi，因此第i段截面刚度由式（2-6）算出：

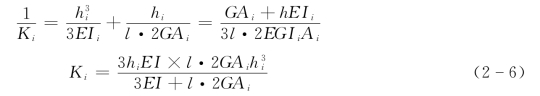
构成的总刚度矩阵为三对角对称矩阵：

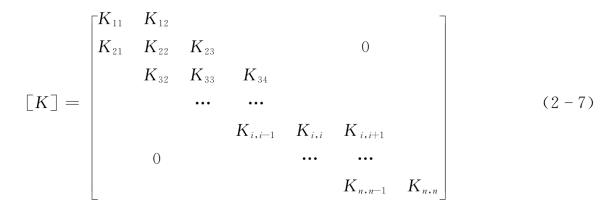
重力坝阻尼比大于一般土建结构，根据实测资料第一阶阻尼比大于5%，接近10%。如果按直接积分法求时程动力反应，常用瑞利阻尼，取为刚度与质量的组合。如果采用振型分解的反应谱法求地震反应，在求自振特性时可以忽略阻尼，计算地震反应时，可选用与重力坝阻尼比相近的反应谱曲线。

用反应谱方法求出各质点的地震荷载为

再将各振型地震荷载作用在质点上，按材料力学方法求出各振型的位移与应力，组合各阶振型的位移应力，就可求得坝体动力反应量。

对于重力坝坝轴向振动，其质量矩阵与上述方法计算的相同。对于重力坝竖直向振动，刚度就不一样了，支承各截面的竖向刚度为Ki=EAi，E为混凝土弹模，Ai第i截面面积，可取每一段的平均截面积。