由于爆炸能量的作用，爆源岩体受强烈挤压拉伸，扭剪产生动态变形，远离爆源之后，这种动变形处于弹性状态，以弹性波形式向四周传播。岩土固相介质中传播的弹性波有体波（Bodywave）和面波（Surfacewave）两大类。体波又区分为纵波 （Longitudinal wave）和横波 （Transversewave），即P波和S波。面波又区分为瑞利波 （Rayleigh wave）和勒夫波（Lovewave）两种。

（1）纵波。纵波，是体波的一种，又称P波，即初波（Primarywave）之意。这种波的介质质点呈压缩——拉伸变形往复移动，质点往复位移的方向与其向远处传播的方向是一致的，由于介质呈压缩和拉伸交替变动形成质点振动，因此纵波也称为膨胀波或压缩波。除此之外，纵波根据其特征还有其他的名称，如由于介质的反复缩伸而呈现疏密状态，所以纵波又称为疏密波；又因为纵波的变形无扭转动，故纵波亦称无旋波；还由于它传播快，最先到达，是初至的波，因此纵波也称为初波。

这种波在地层中传播是很复杂的，为了便于理解传播的机理，可以先讨论完全弹性介质的一维问题。假设有一根等截面的实心棒，长度远大于截面尺度，在截面一端突然施加均布力，截面上会产生压应力σ，棒端截面有压缩变形，其变形沿杆长度方向，向另一端传播，即压应力向另一端面传播。假设其传播速度为CP，经过时间t的传播距离为CPt，长度CPt的一段杆受到压缩，其后压缩变形逐渐向传播方向拓展，在很小的时段内显然压缩区扩展的长度为CPΔt，其压缩量根据应力应变关系可得

式中：E为弹性模量，相应的质点速度v可由式（1-3）求出为

这时这段杆的动量即为

式中：A为杆截面面积；ρ为质量密度。

在Δt时段内，压缩变形扩展段受到的冲量为

冲量与动量相等，即ΔI=ΔM，于是传播速度求出为

波动在上述杆中传播的状况，可以建立一维波的运动微分方程来进行描述。假设杆端受到截面垂直动荷载，杆的变形也完全与力的方向一致，杆的变形与杆的轴线平形，杆的截面在变形时保持为平面。杆的质点位移运动示于图1-3中，设杆件沿轴向的质点位移为u，它是坐标x和时间t的函数。根据杆中脱离体dx两端的受力差与对应这一脱离体dx段运动产生的惯性力相等的原理及应力应变关系σ=Eε，可得出运动微分方程式为

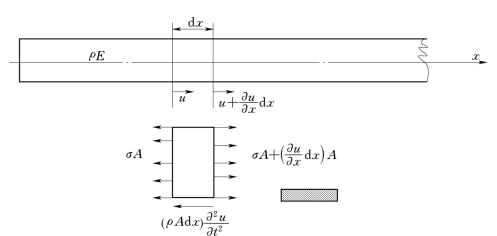
图1-3　杆质点脱离体位移运动示意图

含有（x-CPt）或（x+CPt）的任一函数都是这个方程的解。它的通解可表示为

f1（x-CPt）代表沿x方向传播的波，而f（x+CPt）代表向相反方向传播的波，通解代表两个波，沿x轴以方程式（1-7）所表示的速度CP向两个相反方向运动。可以证明正弦波形

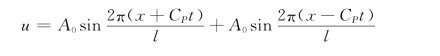
和余弦波形

都是方程的解。式中：A0为振幅；l为波长；CP为纵波波速。

根据式（1-4）与式（1-7）可得出质点速度v与应力σ的关系为

进行变换可得(www.daowen.com)

式 （1-10）说明纵波应力与弹性质点传播速度以及质量密度成正比，而式 （1-11）说明纵波应力与弹性质点振速以及波传播速度的比值成正比，比例常数就是材料弹性模量E。由线弹性的应力应变关系又表明v/CP是波中的动应变。这一极限值与杆的材料力学性质有关。两端自由的杆件，当一端受冲击作用时，杆产生压缩波沿x轴向另一端运动，当压缩波到达另一端面时，波产生反射，形成膨胀波，向x轴相反方向传播，用安装在压杆上的传感器，可以测定出这一波的传播过程和波的方向形态的变化，如图1-4所示。

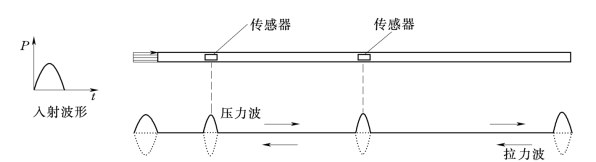
图1-4　杆中应力波传播

在无限弹性介质中传播的纵波，对于点爆破严格说应该是球面波，但远离爆源后，也可近似按平面波处理。它和一维波方法相类似，可以同样建立运动平衡方程，不同的是波速与介质的泊松比有关。

在无空间弹性介质中的波，利用位移表示的微分方程，再加上惯性力，即可得

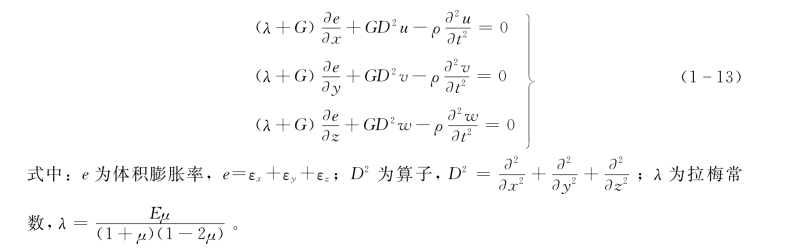
对于压缩波纵波，这里不产生畸变或旋转，方程式（1-13）就变成为

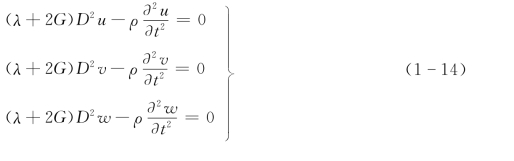
这就是膨胀波的方程。

（2）横波。横波是体波的一种，因为它次于P波到达，所以称为次波或S波；因其质点位移往复运动的方向与波传播的方向垂直，而称为横波。由于这种波能引起介质的畸变，但并无体积变化，故又有剪切波、畸变波、切变波（Shearwave）之称。

介质质点在水平方向产生往复剪切移动的S波称为SH波，如在竖直方向产生往复剪切移动的S波称为SV波。

如同无限弹性介质的纵波，当远离爆心时，横波也可作为平面波处理。假设所有质点的运动都垂直于波传播的方向，波是畸变波。设波沿x轴方向传播，y轴与z轴向位移v=w=0，只有位移u是x与t的函数。这时由方程式（1-13）可得

CS是畸变波传播的速度，它由式（1-16）确定

方程形式与前述方程相同。只是波传播速度比纵波传播速度小。

假设泊松比μ=0.40，则代入式 （1-17）得CS=0.408CP，显然横波波速比纵波波速小很多，通常在地表层纵横波传播接近这一比值。

以上所述的两种波（纵波及横波）都是固体介质中的体波。

（3）瑞利波（Rayleighwave）。这种波是一种在固体介质表面传播的波，它是由于P波在地层中经多次折射在表层形成的。这种波使介质的质点在波传播的方向平行的竖直平面内运动。其轨道为向震源逆进的椭圆，竖直向和纵向有位移，横向无位移。它的传播速度CR比剪切波S的波速CS小，如果泊松比μ=0.5，则CR=0.96CS。瑞利波的一个特点是在半无限体表面振幅大，向深部则迅速衰减，另一个特点是沿传播方向的衰减较慢，可以传播得很远。

（4）勒夫波（Lovewave）。这种波也是一种面波，只在半无限体内有低速表层的情况才存在的一种波，波动的质点运动方向是水平的，与波传播方向成直角。在表层中，x轴和z轴方向的位移u和w 均为零，只有y方向上的位移v沿x轴传播（图1-5）。

勒夫波是SH波在低速表层内多次反射形成的。其波速CL介于表层的CS和基底硬层C′S之间，近似可取两者平均值或两者中的一个值。这种波有在沿深度方向衰减快而在传播方向衰减较慢的特点。

这里还要指出一点，在震源附近一般不会产生面波，只有在离开震源一定距离才形成面波，这个距离可确定如下：①P波形成的瑞利波距离震源应大于；②S波形成的勒夫波距离震源应大于；其中h为震源距地面深度。

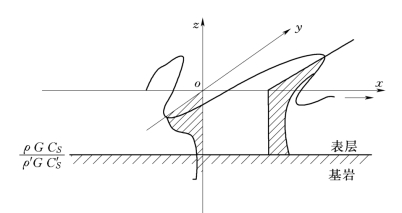
图1-5　面波