以某种疾病及与其相关联的3项指标为例。某种疾病属性设为B1且患病取值为1，否则取为0；其他与其相关联的指标属性分别设为B2、B3、B4，指标值升高取值为1，否则取为0。共764个样本，分为3个数据集，分别为D1，D2，D3，按顺序输入。

（1）首先构建属性原始排序的关联树，并将数据集D1存储在关联树。如图6.4。

图6.4　数据集D1按属性原始排序的关联树

根据关联树数据信息，可得各属性的支持数和支持度。

表6.14数据集　D1各属性的支持数和支持度

按支持数从大到小进行更新属性排序。

表6.15　数据集D1更新属性排序

按更新属性排序，更新数据集D1的关联树。如图6.5所示。

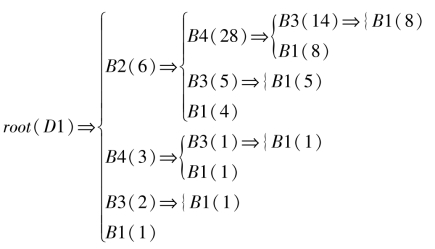
图6.5　数据集D1的更新关联树

由式（6.4.1）可得集合D1的频繁项支持度阈值。2－项频繁集的支持度阈值为0.1994（支持数为18），3－项频繁集的支持度阈值为0.1538（支持数为14）。

根据更新的数据集D1所建的决策关联树，可得候选集的支持数。如表6.16所示。

表6.16　数据集D1候选集的支持数

由频繁项集的子集一定是频繁项集及频繁项集的支持度阈值，可得2－频繁项集及3－频繁项集支持数，如表6.17。

表6.17　数据集D1的繁项集支持数

（2）输入数据集D2。按更新属性排序，如构建数据集D2的关联树，并将数据集D2的信息存储在关联树的各节点。如图6.6。

图6.6　数据集D2关联树

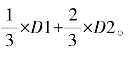给出时效加权系数对数据集D1、D2进行时效加权。按时效加权系数，合并更新数据集D1关联树（图6.5）和数据集D2关联树（图6.6），构建时效加权关联树。关联树各节点的存储信息模型为如图6.7。

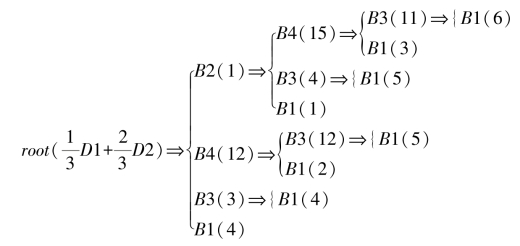
图6.7　数据集D1和D2的时效加权关联树

得到时效加权后的4属性项的支持数及支持度，如表6.18。

表6.18　数据集时效加权后的支持数及支持度

对4属性项按支持度从大到小进行排序，如表6.19。

表6.19　按支持度从大到小更新属性项的排序

由于属性排序发生了变化，更新时效加关联树，如图6.8所示。

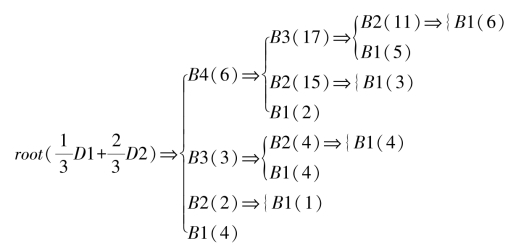
图6.8　更新时效加关联树(www.daowen.com)

根据更新时效加权关联树（图6.8），可得候选集的支持数。如表6.20所示。

表6.20　时效加权后频候选繁集的支持数

由式（6.4.1）及数据集D1、D2的更新时效加权关联树，可得2－项频繁集的支持度阈值为0.24（支持数为21），3－项频繁集的支持度阈值为0.1478（支持数为13）。

2－频繁集、3－频繁集如表6.21。

表6.21　时效加权后频繁集的支持数

（3）输入数据集D3。重新赋值时间节点，即t2＝t1，当下时间为t2，重新定义数据集标签，即

按更新时间节点后定义的属性排序（表6.18），构造数据集D2的关联树，按时效加权模型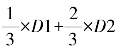合并数据集D1关联树和数据集D2关联树，如图6.9。

图6.9　合并的关联树

由时效加权关联树可得各属性项的支持数和支持度，如表6.22。

表6.22　时效加权关联树计算得到的各属性项的支持数和支持度

对照表6.18与表6.21的属性项排序，可以判断属性排序无变化。

由表6.21计算时效加权得到的频繁集的支持度阈值，2－项频繁集的支持度阈值为0.1593（支持数为14），3－项频繁集的支持度阈值为0.1249（支持数为11）。

由关联树可得各候选集的支持数和支持度。如表6.23。

表6.23　候选集的支持数和支持度

由支持度阈值可得2－频繁项集、3－频繁项集，如表所示6.24。

表6.24　频繁集的支持数和支持度

输入数据集D1并进行关联分析，B1与指标B2、B4关联；

输入数据集D2并进行时效加权关联分析，B1与指标B2、B3、B4都无关联；

输入数据集D3继续进行时效加权关联分析，B1与指标B3、B4关联，而指标B1与B2无关联。

由此可以得出结论，该数据集是存在概念漂移的，并从这3个数据集的分析结果可以得出，该种疾病与指标B4关联的性质较为稳定，而与指标B2关联不够稳定。

上述的算法，可以看出，对数据集仅仅需要一次遍历，需要存储数据的空间较小，关联树的数据信息保留了较多的信息量，同时关联树的数据存储结构便于新输入数据的寻址。

该关联树各节点的存储数据都是单路径，如图6.6中关联树节点B2－B3（4），表示的数据集D1中当且仅当属性项B2和B3的取值为1的事务个数，该节点存储的4个事务取值都是｛0　1　1　0｝，且数据集D1中的取值为｛0　1　1　0｝的事务都存储在该节点中。关联树的每个节点存储不同的取值的事务频数。该存储结构的优势：

（1）关联树各节点显示的信息特征清楚，不依赖于其他节点存储信息。

（2）便于事务寻址，提高运算速度。

（3）节省存储空间，提高存储数据特征的信息量。

（4）便于数据流的输入，便于数据集的加权合并。

（5）当数据概念漂移更新关联树时，不用对旧数据的再一次遍历，而是从关联树中可以得到旧数据的所有取值信息。

（6）根据时效或功效的大小进行加权，既没有将历史数据或关注度低的数据遗弃，也充分考虑了“数据的重要性”对关联问题的影响。