关联规则为用户带来了巨大的商业利益，大部分关联规则算法都假定数据库中每个项目都具有相同的重要性，然而实际情况并非如此。首先，随着时间的推移，数据库中的数据的时间跨度越来越大，然而不同的项目在数据库中的分布是不均匀的，有些项目的时间跨度可能超过十年，也许某些项目是刚刚开始出现的，例如对一个电器商场而言，“录音机”在20世纪末，是时髦商品，但到2005年后“录音机”变成了滞销品，取而代之的是新的高科技产品，如“MP3”，很明显包含“MP3”的规则要比包含“录音机”的规则重要得多。由于“录音机”在2005年以前曾经长时间的旺销，因是在数据库中的支持度很高；另一方面，由于“MP3”刚刚出现在市场上，其销量在整个数据库中占很小的份额，即支持度很低，所以，传统的关联规则挖掘算法所发现的规则将包含“录音机”，而不会包含“MP3”。这就是所谓的时间效应问题，即历史越久远的数据应该对规则的影响越小，现有的算法无法解决该问题。

其次，用户对某些项目可能更感兴趣，希望在进行挖掘时能够增加它们的作用，同时削弱另外某些项目的作用。例如对一个商场来说，“铂金钻戒”和“高级香水”是贵重商品，其利润要远远高于日用商品“牛奶”和“面包”，由于“铂金钻戒”和“高级香水”的单价很高，所以销售量很低，即在数据库中的支持度很小，是一个非频繁项集，因而即使“铂金钻戒”⇒“高级香水”是一条置信度很高的规则，也会因为｛“铂金钻戒”，“高级香水”｝是非频繁项集而被传统的关联规则挖掘算法所忽略。与此相反，“牛奶”和“面包”的销售量很大，是频繁项集，它们将被包含在挖掘出来的规则中，但是商家也许可能会更关心有关“铂金钻戒”和“高级香水”的情况。

为了解决上述问题本书作者引入时效加权关联规则和功效加权关联规则的概念，将加权支持度的计算模型进行变形处理，引用k－频繁项支持期望作为频繁项支持度阈值，省去计算各项集加权支持度，再与最小加权支持度进行对比的过程。

6.4.3.1　时效加权支持度算法

假设T＝｛t1，t2，…，tn｝是一组n个不同的时间间隔的集合，设ti＝［s，c］是一个时间间隔，其中分别ti·s和ti·c表示ti开始与结束且ti·c≤ti＋1·c。

假设I＝｛i1，i2，…，im｝是一组m个不同项目的集合。给定一个交易集合D，其中每个交易由下列属性组成：交易时间以及用户在该交易中所购买的所有项目，交易时间用T.time，其中任一个交易的交易时间Tt.time∈T，显然t1就是最早的交易时间间隔，tn就是最晚的时间间隔。

显然越早发生的事务，其重要性就越小，应当降低它对规则的影响，相反，应当加强近期发生的事务对规则的影响。给定一个数据集合D和D上的时间间隔集合T，可以对每个时间间隔设置一个时效的权值vi（0≤vi≤1，i＝1，2，…，n），这里n为T中时间间隔的数量，对一个交易T，如果T的交易时间落在时间间隔ti内，即ti.s≤T.time≤ti＋1.c，则称T在区间ti内有时效的权值vi。如果项集X⊆T，那么X在区间ti内也有时效的权值vi。由此定义项集X的时效加权支持度，即

式（6.4.2）中，Count（Xi）是时间区间ti中包含项集X的交易数，Nv为加权后的总交易数，即

式（6.4.3）中，Ni是时间间隔ti中的交易数。

对一个项集X，如果X的时效加权支持度不小于minsup，称X为时效频繁项集VFI（Vertical Frequent Itemset），否则，称X为时效非频繁项集VIFI（Vertical Infrequent Frequent Itemset），如果规则X⇒Y的时效加权支持度和置信度分别大于或等于minsup和minconf，称X⇒Y为时效有用规则。(www.daowen.com)

这里需要说明的是，有些数据随着时间的推移对规则的影响越来越小，而且当达到一定时间以后对规则几乎没有影响，也就是说，数据信息的作用是有实效性的。故为了减少算法所需的存储空间，对规则失去效应的数据进行舍弃，不妨设T＝｛t1，t2，…，tn｝为有效数据的时间间隔。如设时间ti＋1＝ti＋Δt（i＝11，2，…，n－1），tn为当前时间。每过去一个时间段Δt，t1时间段的数据信息将被删除。时间变量重新赋值，即“ti－1＝ti”。

关联树的节点的存储信息加入数据输入的时间标签ti。这样关联树每个节点的存储变量为X1，X2，…，Xn，其中Xi为时间标签ti时间段输入的数据。则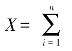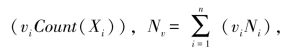即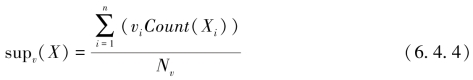

6.4.3.2　功效加权支持度算法

某些时候用户可能对某些项目更感兴趣，希望加强这些项目对规则的影响，而对另外一些项目不感兴趣，要求削弱这些项目的作用，为此可以对不同的项目设置不同的权，对用户有兴趣的项目设置较大的权值，其他不重要的项目则设置较小的权，称这种问题为功效加权关联规则问题。

给定一个项集I＝｛i1，i2，…，im｝，对每个项目ij设置一个功效的权值hj，其中0≤hj≤1（j＝｛1，2，…，m）。定义项集X的功效加权支持度如式（6.4.5）所示

式（6.4.5）中，sup（X）为X的支持度，k是项集X的维数，即X中所包含项目的个数。我们把会把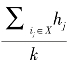叫X的功效权值，记作显hx，显然0≤hx≤1。

6.4.3.3　改进的频繁项支持度阈值

将加权支持度的计算模型进行变形处理，引用k－频繁项支持期望作为频繁项支持度阈值。设对Ai项的关注度为hAi，则定义改进的功效加权支持度为hAiPAi，频繁项支持度阈值为