传统的关联规则挖掘算法大多没有对事务数据库进行处理，直接读取事务数据库，即采用水平数据布局数据库形式。当事务平均宽度较长时或设定的支持度阈值较低时，频繁项集数量指数增长，原始的事务数据库中数据量则更加巨大，这种海量数据不可能一次性存入内存中，而只能放在辅助存储器中暂存。

对于关联规则挖掘算法，我们并不关心一个事务的数据列表信息，而是关心事务数据库中的频繁项的信息，所以本文采取树形的存储结构来存储各频繁项信息，并采取对事务只扫描一次的扫描形式。不记录且不保存事务的信息，但记录并保存该事务对前期事务数据库频繁集的作用。

为了更清楚地进行关联规则挖掘问题的讨论，假设原始的事务数据库如表6.11所示，这是一个水平数据布局事务数据库，对原始的事务数据库进行一次遍历。

表6.11　事务数据库

设事务数据库矩阵形式为

表示事务项形式的数据库支持计数如表6.12所示。

表6.12　事务项形式的数据库支持计数

首先对各项按支持计数从大到小进行排列，其结果如表6.13所示。

表6.13　各项按支持计数从大到小进行排列

更新设事务数据库矩阵形式

(www.daowen.com)

然后建关联树。

按表中项的顺序建立第一节点；对于每一个第一层节点继续生成下一层的节点，其生成原则是排在该项后面的项为第二层节点，如C项的下一层节点只能是E和D两个节点，以此类推，继续生成第三层等，直到叶节点。

依据存储树的各存储节信息特征互斥的原则，可得存储树的个节点存储信息。关联树建成后，输入事务数据库，每一个节点作为一个存储点，存储该节点所对应项是事务取值为1的最后一项的个数。

对于事务按表中顺序，第一个取值为1的项为第i项，则进入到第一层的第i项节点；第二个取值为1的项为第j（i＜j）项，则进入到第一层第i项节点后的第二层的第j项节点，以此类推。

如序号为2的事务取值为（1　1　0　0　0　1），事务的项为BFA，第一层是B节点，第二层是BF节点第三层为BFA节点，而且该事务最后取值为1的项是A，即BFA节点存储计数增加1，以此类推。如图6.3。

各存储点的数值为该项的频数，如上面树的第二层第一个节点B（0），即为事务项B的频数为0；第一项为B的所有事务项的频数为

B（0）＋BF（1）＋BFA（1）＋BFAC（1）＋BFAD（1）＋BA（0）＋BAC（1）＋BC（1）＝6

再如第三层的第1个节点F（1），即为事务项最后取值为1的项是F的频数为1；而所有含BF的事务项的频数为

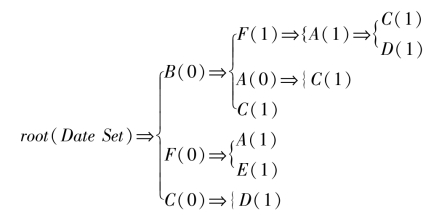
图6.3　IAW关联树示意图

频繁项集BF的支持度为4／9，可信赖度为4／6。

IAW关联树与FP关联树的区别在于各节点的存储信息不同。FP关联树每个子节点存储的事务数量都是上一层父节点的子集，即父节点存储事务个数等于其下一层子节点存储事务个数之和。IAW关联树每个节点存储的事务数量之和等于树根数据集事务总量，也就是说，每个事务只在一个节点计数，每个节点的事务存储路径都是相同的，每个节点的事务数据特征更清晰。

对于可变数据量的动态数据库，该IAW关联树不用剪枝。