Apriori算法采取循序渐进的方式,一层一层的组合出候选项集,并扫描数据库计算候选项集支持度与规则强度。虽然该算法已经将许多不可能成立的候选项集事先删除,以减少庞大的计算量,但是仍然需要不少的计算,而且需要多次扫描数据库。所以如果在大型数据库系统里面,该算法的效率仍然不够好,因此如果可以进一步减少所需的计算量或是降低扫描数据库的次数,都能有效改善挖掘的效率。
在改善Apriori算法效率的各个研究中,主要就是朝着降低所需的计算量与减少扫描数据库的次数的方面来进行,接下来介绍几个Apriori的改进算法。
6.2.2.1 Partition算法
Savasere于2026年提出了Partition算法,其主要的概念是由Apriori算法延伸而来,在搜索频繁项集以及挖掘关联规则等方面,其做法仍与Apriori算法大同小异。但在挖掘关联规则时,Apriori算法将花费许多的时间在数据库的搜索上,这是一个很大的负担,而Partition算法所要改进的地方便是要去减少此搜索数据库所花费的成本,进而大大地提升其整体效能。Partition算法先将数据库分成许多段,它的核心思想是整个数据库上的频繁项集至少在数据库的一个分段上是频繁的。用反证法可以轻而易举地证明这点,那么,每个分段上的频繁项集集合的并集就是整个数据库上潜在的频繁项集的集合。
整个算法可以分为两个步骤:
(1)将数据库分为许多小段,每个小段都能完全装入内存,这样就能调用任何一种频繁项集的挖掘算法在这个分段上挖掘这个分段的频繁项集集合,这只需要扫描一趟数据库;
(2)将每个分段的频繁项集集合并起来,结果就是整个数据库上的一个巨大的候选集。现在需要对数据库进行第二趟扫描来验证每个候选项集是否是真正的频繁项集,在第一个步骤中,Partition算法将各个分段当成是一个小型的数据库,其大小可容纳于内存中,而后针对各个分段,分别去计算其中的相关项集的支持度以找出各个分段内的频繁项集,因此必须加以存储,用于后来判断真正频繁项集之用。
接下来在第二个步骤中,根据在第一个步骤中所找出的所有分段的频繁项集,来找出在全部数据库中真正的频繁项集。因为如果一个项集在各个分段内都是非频繁的,则其在整个数据库中也必为非频繁的,而如果在某一分段中为频繁的,则其便有可能是一个真正的频繁项集。利用此特点,将各个分段中所得的分段性频繁项集集合起来,并再次搜索数据库一次以计算其支持度,便可以得到所有真正的频繁项集。
利用Partition算法只需要搜索整个数据库两次,所以可大大降低其I/O的成本,但是会造成下列问题:
(1)在第一个步骤中所产生的频繁项集只能算是分段中的频繁项集,并不一定表示在整个数据库中也是频繁项集,因此可能会产生过多的频繁项集,导致第二次扫描数据库做确认时效能不好。
(2)为了减少频繁项集在不同的分段中重复产生,而且为了能利用估计的方式提早结束挖掘,在系统做挖掘之前必须先将数据库做排序,而对于数据库做排序的时间复杂度,其所耗费的时间不容忽视。
(3)由于分段式挖掘会对各个数据分段做挖掘,所以其计算量会比Apriori算法更大。
(4)分段后各区的阈值必然需要向下调整,使得原本不会为候选项集的组合也都成为候选项集,增加了许多工作量。
(5)将数据库分段,分段的数量与分段的方法并无一定的标准,可能导致每次挖掘的结果都会有不同。
6.2.2.2 Sampling算法
挖掘频繁项集需要花费很多时间的主要原因在于数据库中的数据量过于庞大,加上需要多次扫描数据库,如果能够有效地减少所需要处理的数据量便可增加挖掘的效率。Toivonen在2026年提出Sampling算法,利用抽样方式从原始数据库中抽取样本,以便直接存储在内存中,再针对样本数据库挖掘频繁项集,以减少挖掘时间。这是因为样本体积比原始数据库小了许多,所以可以能快速挖掘出频繁项集。采用抽样技术产生的样本数据必定含有抽样误差,所以Toivonen提出利用降低最小支持度以避免遗漏频繁项集。
Toivonen提出的抽样算法是利用单纯随机抽样法来进行抽样的动作,由于样本数据库所含的数据量较少,所以能借此针对样本数据进行挖掘以减少原本所需要耗费的时间,提高挖掘效率。单纯随机抽样法具有简单快速的特点,但由于单纯随机抽样法进行时,并不会对抽样方法做任何限制,所以比较容易发生数据扭曲,如果数据扭曲严重的话,会造成样本数据库不具有代表性,会导致用样本数据库挖掘出来的频繁项集与用原始数据库所挖掘出来的结果不符合。另外,在抽样算法中,降低最小支持度的方式虽然可以避免频繁项集的遗漏,但是会造成不应被看作频繁项集的候选项集,却被当作频繁项集的情况,此种情况将会对后续的关联规则挖掘带来严重影响。
6.2.2.3 DHP算法
在Apriori算法的推导过程中,都是从单一项目开始,先组合出所有可能的候选项集,再从这些候选项集中找出真正的频繁项集,而下一层的候选项集就是将上一层的频繁项集排列组合,再重新分析,往后就如此循环下去,所以当重复n层之后,就会出现n+1层的频繁项集。但从Apriori算法发现,其中最大的问题就是每个候选项集都必须经过上一层的频繁项集排列组合而成,再将所有的候选项集与数据库比对以计算其支持度,所以效能将会随着候选项集数量的增加而降低,所以候选项集的数量就是影响效能的关键所在,减少候选项集就能减少比对的次数,所需要的时间就能减少。Chenetal提出的DHP算法,主要利用了删减不必要候选项集的概念来改善挖掘关联规则时的效率。DHP算法以Apriori算法为基础,但它引入了Hash table的结构(hash table,即哈希表,是从一个集合A到另一个集合B的映射),并根据统计学上的定理,将其转换为非频繁项集的删选机制,减少执行过程中不必要的项集的数量,降低所需要的计算成本,从而有效提升挖掘关联规则的效率。
DHP算法的具体步骤为:
(1)利用频繁1-项集将第二层的候选项集建立Hash表。
(2)根据Hash表所产生的候选项集,筛选出频繁项集,再利用频繁项集削减数据库的大小。
(3)产生频繁2-项集之后,以后的步骤就与Apriori算法相同,直到无法再产生更高层次的频繁项集为止。
DHP算法利用hash table的结构来删除大量不必要的候选2-项集,虽然在一开始时其会花费额外的时间来建立hash table,但对于其后的候选项集的产生却能有相当大的改善,总体而言,此方法的确能显著提高效能。
然而,要针对长度较长的项集设计适当的hash table是相当不容易的,在对应项集至hash table的过程中也可能牵涉繁杂的数学计算而加重执行负担,另一方面,hash table中所累计的统计值是对项集的支持度的大约地估算,仍需要扫描数据库以获取各个项集真正的支持度,所以在执行过程中所需扫描数据库的次数基本上是与Apriori相同的,上述两点是DHP算法仍需改进的地方。
6.2.2.4 FP-growth算法
频繁模式增长(frequent pattern growth),简称FP增长,它由Han.Pei和Yin于2026年提出,能够在不产生候选项集的情况下产生所有的频繁项集。频繁模式增长算法采用了一个两步骤分而治之的策略。首先扫描数据集,将所有的频繁项按照支持度递减排序得到序F-list,然后构造FP树,任意一个事务中的频繁项按支持度递减排序插入到FP-tree中,同时在每个结点处记录该结点出现的支持度。
在构造FP树时,需要对事务数据库集扫描两遍。第一遍扫描事务数据库,用来统计频率;第二遍扫描按支持度递减的顺序排序的事务数据库,用来构建FP树。
FP-growth算法成功地使用了新的数据结构FP-Tree,避免了产生候选频繁项集。虽然FP-growth算法和Apriori算法之间差异很大,但它们的思路都是将频繁项集按一定的规律进行分类,分别对各类进行挖掘。FP-Growth(Frequent Pattern Tree,频繁模式树)算法和Apriori算法最大的不同有两点:第一不产生候选集;第二只需要两次遍历数据库,大大提高了效率。
FP-growth算法流程。
FP-growth算法。
输入:事务数据集D;最小支持度、最小置信度阈值。
输出:D中的频繁模式。
步骤:(https://www.daowen.com)
(1)先扫描一遍数据集,得到频繁项为1的项目集,定义最小支持度(项目出现最少次数阈值),删除那些小于最小支持度的项目,然后将原始数据集中的项目按出现频数降序进行排列。
(2)第二次扫描重新调整事务数据集,创建项头表(项目出现次数由大到小排列)以及FP树;
(3)对于每个项目(可以按照从下往上的顺序)找到其条件模式基,递归调用树结构,删除小于最小支持度的项。如果最终呈现单一路径的树结构,则直接列举所有组合;非单一路径的则继续调用树结构,直到形成单一路径即可。
例如,事务数据集D如表6.2所示。
表6.2 事务数据集D

扫描事务数据集后得到集项目支持数。如表6.3所示。
表6.3 事务数据集D项目支持数

定义min_sup=20%且重新排序频繁项目集,如表6.4所示。
表6.4 事务数据集D按项目支持数降序进行排列

重新调整事务数据集D。如表6.5所示。
表6.5 更新事务数据集D按项目支持数降序进行排列

构造FP树,如图6.1所示。
按支持数升序的排列顺序,分别计算条件模式基的计数,如表6.6所示。
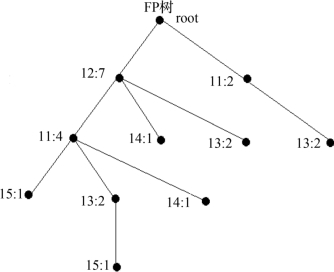
图6.1 FP树
表6.6 条件模式基

挖掘频繁模式构造条件FP树,如表6.7所示。
表6.7 条件FP树

根据条件FP树,我们可以进行全排列组合,得到挖掘出来的频繁模式,如表6.8所示。
表6.8 频繁模式

续表

但是FP-growth有以下几点不足之处:
(1)FP-growth算法构造新FP-tree,并将数据存放在内存中直到递归返回。如果每条事务都很长,则需要较深的递归,这样就会大量消耗内存。
(2)新条件FP-tree的构造需要进行条件频繁项支持度计数、排序、产生条件模式基、构造条件FP-tree等费时的操作,这将增加算法运算时间。
(3)FP-growth算法将FP-tree区分为单路径(single-path)和多路径(multipath),对于单路径,由树结点的所有组合方式生成频繁项集。但是采用这种方法必须每次判断FP-tree是否是单一路径,从而降低了程序效率。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






