Apriori算法是现今研究关联规则中最具代表性的方法。Apriori算法利用层次顺序搜索的循环方法（又称作逐层搜索的迭代方法）来完成频繁项集的挖掘工作，同时利用下面的Apriori定理来压缩搜索空间，提高频繁项集产生的效率。

Apriori算法的基本思想是生成特定规模的候选项集，然后扫描数据库并进行计数，以确定这些候选项集是否频繁项集。具体实现过程是首先扫描数据库的所有事务，计算每个项目的发生次数，产生候选1－项集C1，再根据预先给定的最小支持度确定频繁1－项集L1。然后由给出L1⊗L1，进行连接运算生成候选2－项集C2，再次扫描数据库中的所有事务，计算出C2中每个元素的出现次数，并根据预先给定的最小支持度确定频繁2－项集L2。这一过程反复进行直到生成频繁k－项集Lk，并且不可能再生成满足最小支持度的（k＋1）项集。在这个循环过程中，对于候选j－项集C，（j＝3，…，k），若其中某个元素的（j－1）子集不是频繁（j－1）－项集，将被删除掉。

下面具体给出Apriori算法。

首先，通过扫描数据库，累积每个项的计数，并收集满足最小支持度的项，找出频繁1－项集的集合，该集合记为L1，然后L1与L1连接得到候选2－项集C2。对C2计数，找频繁2－项集L2。通过频繁（k－1）－项集连接得到k－项集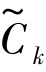（k＞2），对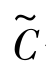使用定理：频繁k－项集的（k－1）项子集都是频繁项集对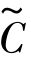进行剪枝，得到候选k－项集Ck，对Ck进行计数得到频繁k－项集Lk。如果频繁k项集非空，则继续连接生成（k＋1）－项集。

Apriori算法流程。

算法：Apriori

输入：事务数据库D；最小支持度、最小置信度阈值；

输出：D中的频繁项集L

（1）扫描数据库，生成候选1－项集和频繁1－项集。

（2）从2项集开始循环，由频繁（k－1）－项集生成频繁k－项集。

Ⅰ.频繁（k－1）－项集生成2项子集。(www.daowen.com)

Ⅱ.对由（Ⅰ）生成的2项子集中的两个项集根据上面所述的定理（1）进行连接，生成k－项集。

Ⅲ.对k－项集中的每个项集根据如上所述的定理（2）进行计算，舍弃掉子集不是频繁项集即不在频繁（k－1）－项集中的项集。

Ⅳ.扫描数据库，计算（Ⅲ）步中过滤后的k－项集的支持度，舍弃掉支持度小于阈值的项集，生成频繁k－项集。

（3）当前生成的频繁k项集中只有一个项集时循环结束。

基于频繁项集的Apriori算法采用了逐层搜索的迭代的方法，算法简单明了，没有复杂的理论推导，也易于实现。但是它存在一些难以克服的缺陷：

（1）对数据库的扫描次数过多。在Apriori算法的扫描中，每生成一个候选项集，都要对数据库进行一次全面的搜索，如果要生成最大长度为k的频繁项集，那么就要对数据库进行k次扫描。当数据库中存放大量的事务数据时，在有限的内存容量下，系统I／O负载相当大，每次扫描数据库的时间就会很长，这样效率就非常低。

（2）Apriori算法可能产生大量的候选项集。在规模较大的情况下，Apriori算法需要产生大量的候选项集。如果有104个频繁1－项集，则需要产生107个频繁2－项集。

（3）在频繁项集长度变大的情况下，运算时间显著增加。当频繁项集长度变大时，支持该频繁项集的事务会减少，从理论上讲，计算其支持度所需要的时间不会明显增加，但Apriori算法仍然是在原来事务数据库中来计算频繁项集的支持度，由于每个频繁项集的项目变多了，所以在确定每个频繁项集是否被事务支持的开销也增大了，而且事务没有减少，因此频繁项集长度增加时，运算时间显著增加。

（4）采用唯一支持度，没有考虑各个属性重要程度的不同。在现实生活中，一些事务的发生非常频繁，例如面包，对商家来说利润很低，而有些事务则很稀疏，例如铂金钻戒，对商家来说利润却很高，如果将他们同等进行处理，显然对利润高的商品是不公平的。

（5）算法的适应面窄。该算法只考虑了单维布尔关联规则的挖掘，但在实际应用中，可能出现多维的、数量型的、多层的关联规则。这时，该算法就不再适用，需要改进，甚至需要重新设计算法。