关联规则就是在给定训练项集上频繁出现的项集与项集之间的一种紧密的联系。其中“频繁”是由人为设定的一个阈值即支持度（support）来衡量，“紧密”也是由人为设定的一个关联阈值即置信度（confidence）来衡量的。这两种度量标准是频繁项集挖掘中两个至关重要的因素，也是挖掘算法的关键所在。对项集支持度和规则置信度的计算是影响挖掘算法效率的决定性因素，也是对频繁项集挖掘进行改进的入口点和研究热点。

6.1.2.1　相关概念

项的定义：事务数据库中的一个属性字段，每个字段有一定的取值范围。如对超市数据来讲，项是指交易中的特定商品。

项集定义：包含若干个项的集合。

项集维数定义：把一个项集所包含的项的个数称为此项集的维数或项集的长度，长度为k的项集，称为k－项集。

2项子集定义：频繁（k－1）－项集生成2项子集，这里的2项子集指的是生成的子集中有两个（k－1）－项集，如使有3个2－项频繁集｛a，b｝，｛b，c｝，｛c，f｝，则它所有的2项子集为｛｛a，b｝，｛b，c｝｝，｛｛a，b｝，｛c，f｝｝，｛｛b，c｝，｛c，f｝｝；

项集的支持度的定义：设I＝｛I1，I2，…，Ip｝是p个不同项目的集合，假定X是一个项集，且X⊆I，D＝｛x1，x2，…，xn｝是一个事务集合或事务数据库，称D中支持项集X的个数（称为项集X的支持数，记为Count（X））与D中总的交易个数之比为X在D中的支持度，记作Supoort（X），即

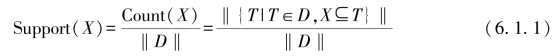
关联规则的支持度的定义：关联规则X⇒Y的支持度是事务数据库D中支持规X∪Y项集的个数（称为关联规则X⇒Y的支持数，Count（X⇒Y），占事务数据库D的个数的百分比，记为Support（X⇒Y），即

最小支持度定义：由用户定义的衡量项集频繁程度的一个阈值，记作min＿sup；

频繁项集定义：对一个项集X，如果X的支持度不小于最小支持度，即Support（x）≥min＿sup，称X为频繁项集。

非频繁项集定义：对一个项集X，如果X的支持度小于最小支持度，即Suppor（X）＜min＿sup，称X为非频繁项集。

极大频繁项集定义：不存在包含当前频繁项集的频繁超集，则当前频繁项集就是极大频繁项集。

置信度定义：对形如X⇒Y的关联规则，其中X和Y都是项集，定义规则的置信度为事务集合D中支持项集X∪Y的事务个数与D中支持项集X的事务个数之比，或者说是项集X∪Y的支持度与X的支持度之比，记作Confidence（X⇒Y），即

最小置信度（minimum confidence）：用户定义的一个置信度阈值，表示规则的最低可靠性，记作min＿conf。

候选项集：用来获取频繁项集的候选项集，候选项集中满足支持度条件的项集保留，不满足条件的舍弃。

关联规则可以用支持度和置信度来很好地判断其有效性和可信度。

支持度确定规则所表示的数据在整个数据集中出现的频繁程度。支持度是一种重要度量，因为支持度很低的规则可能只在整个数据集中偶然出现。从商务角度来看，支持度低的规则一般不会有很大的价值，比如对顾客很少同时购买的商品进行促销一般不能产生利润。因此，支持度通常用来删去那些不令人感兴趣或者价值不大的规则。(www.daowen.com)

置信度表示Y在包含X的事务中出现的频繁程度，置信度可以度量通过规则进行推理的可靠性。对于给定的规则X⇒Y，置信度越高，Y在包含X的事务中出现的可能性就越大。置信度也提供在Y给定X下的条件概率的估计。

关联规则发现：对于给定的事务数据集D，关联规则发现是指从D中挖掘出支持度和置信度分别大于等于min＿sup和min＿conf的所有规则，其中min＿sup和min＿conf是对应的支持度和置信度阈值。

6.1.2.2　两个定理

（1）连接定理：若有两个（k－1）－项集，每个项集按照“属性－值”（一般按值）的字母顺序进行排序。如果两个（k－1）－项集的前（k－2）个项相同，而最后一个项不同，则证明它们是可连接的，即这（k－1）－项集可以联姻，即可连接生成k－项集。如有两个3－项集：｛a，b，c｝和｛a，b，d｝，这两个3－项集就是可连接的，它们可以连接生成4－项集｛a，b，c，d｝。又如两个3－项集｛a，b，c｝和｛a，d，e｝，这两个3－项集显示是不能连接生成4－项集的。

（2）频繁子集定理（Apriori定理）：频繁项集的所有非空子集也一定是频繁的。频繁项集也称作是向下封闭的，因为如果一个项集满足最小支持度的要求，其所有子集也满足这一要求。

例顾客购物的记录数据如表6.1。

表6.1　用户购物的记录数据表

续表

表6.1中是顾客购买记录的数据库D，包含6个事务，即‖D‖＝6。项集I＝｛网球拍，网球，运动鞋，羽毛球｝。设X＝｛网球拍｝，Y＝｛网球｝，考虑关联规则X⇒Y。事务1，2，3，4，5，6包含网球拍，即X的支持数Count（X）＝5；事务1，2，5，6包含网球，即Y的支持数Count（Y）＝4；事务1，2，6同时包含网球拍和网球，即关联规则X⇒Y，X的支持数Count（X⇒Y）＝3。所以关联规则的X⇒Y支持度为

关联规则X⇒Y的置信度为

若给定最小支持度α＝0.5，最小置信度β＝0.6，即X和Y都是频繁项集，并认为购买网球拍和购买网球之间存在关联。

6.1.2.3　生成频繁项集及生成规则

一种原始的关联规则挖掘方法是计算所有规则的支持度和置信度，再删去支持度或置信度不满足阈值的规则。因为从数据集中提取的规则数目是指数级，这种方法的计算任务繁重，过高的代价使得它在很多场合下变得不可行。研究者通过对关联规则挖掘的研究发现，很多规则是没有必要计算的，仅仅计算可能满足要求的规则，可以节省大量的时间。目前通常采用一种策略是将关联规则挖掘任务分解为如下两个主要的子任务：（1）生成频繁项集，其任务是生成所有满足最小支持度阈值的项集，这些项集被称作频繁项集（Frequentltemset）；（2）生成规则，其任务是从上一步生成的频繁项集中提取所有高置信度的规则。

通常用格结构来表示所有可能的项集。一个包含k个项的项集最多可能产生2k－1个非空频繁项集。由于在许多实际应用中k的值可能非常大，需要查找的项集搜索空间可能是指数规模的。通常采用减少候选项集的数目和减少比较次数用来存储候选项集或者压缩数据集，以此来替代将每个候选项集与每个事务相匹配，从而可以减少比较次数。

频繁项集是满足支持度阈值的项集，对这些项集再增加置信度的要求，即可从数据集中挖掘出满足要求的关联规则。相对频繁项集生成而言，规则的生成较为简单和直观。通常，生成频繁项集所需的计算开销远大于生成规则所需的计算开销。目前，对关联规则挖掘的研究主要集中在提高频繁项集生成的效率上。