灰色聚类分析作为灰色系统理论的重要组成部分，一直是人们讨论和实际应用较多的灰色技术之一。在传统灰色白化权聚类算法的基础上，很多专家和学者对其进行了改进。

现有的改进算法大多是在三角白化权函数的角度或从权重的角度进行改进，或将传统灰色聚类直接应用到实际问题当中。针对传统白化权函数存在的缺点，本书作者通过引入Logistic（逻辑斯谛曲线）函数，将传统白化权函数进行改进，建立Logistic白化权函数，得到改进的Logistic白化权聚类算法。

通常情况下，灰色白化权聚类算法中的白化值选取只是通过经验定义累积频率曲线百分率来确定，通常不够合理。我们知道，累积频率曲线是单调增的，在类的分界点处的累积频率变化速率相对较慢。由类分界点的性质可得在类的分界点的二阶差分值趋于0，且类分界点左侧的二阶差分小于0及右侧二阶差分大于0。故选取累积频率曲线中拐点为白化值，即类区间临界点。

5.5.2.1　简述Logistic函数性质

Logistic函数是一种常见的S形函数，该函数曲线起初阶段大致是指数增长；然后开始变得饱和，增长的速度变慢；最后，达到成熟时渐进停止增长。它的输入范围是－∞→＋∞，而值域刚好为（0，1），满足概率分布为［0，1］的要求，且是一个单调上升的函数，具有良好的连续性。故本书作者引入Logistic函数，将传统白化权函数进行改进，建立Logistic白化权函数。见图5.10，从而得到改进的白化权聚类方法。

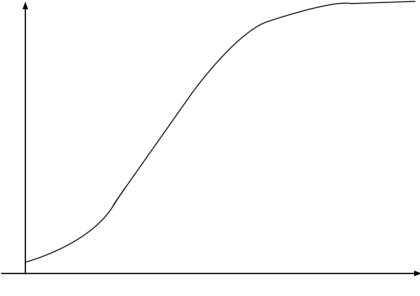
图5.10　Logistic函数曲线

设Logistic函数为

对f（x）求一阶导数，有

对f（x）求二阶导数，有

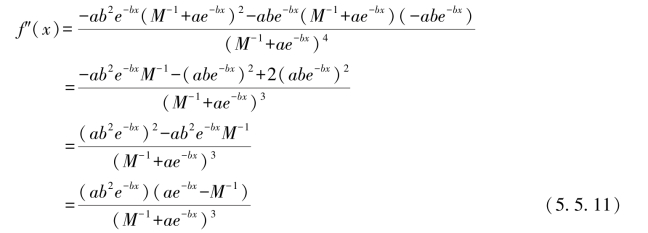
令f″（x）＝0，得ae－bx－M－1＝0，得

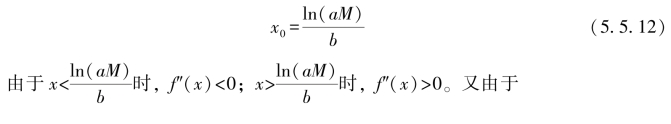
由此可得b越大，在拐点处斜率越大。

由上述对Logistic曲线的推导可得，可以通过调整b的大小来调整白化权函数曲线的形状。

5.5.2.2　Logistic白化权函数的模型建立

（1）Logistic曲线函数：

（2）将f（x）图形以x轴为对称轴进行翻转，得到下面函数：

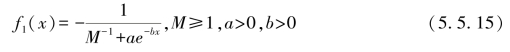
函数f1（x）的曲线图如图5.11所示。

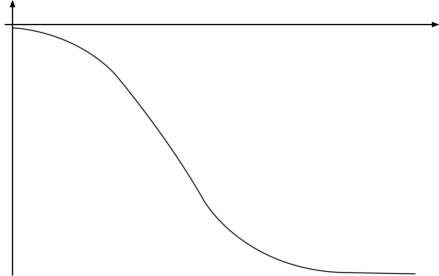
图5.11　函数f1（x）曲线

（3）将f1（x）图形以y轴为对称轴建立对称曲线，得到下面函数：

函数f2（x）的曲线图如图5.12所示。

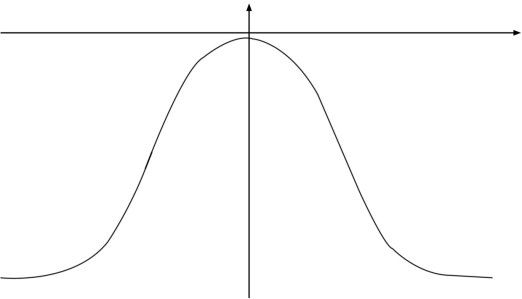
图5.12　函数f2（x）曲线

（4）将f2（x）图形向上平移c个单位，并向右平移d个单位，得到下面函数：

函数f3（x）的曲线图如图5.13所示。

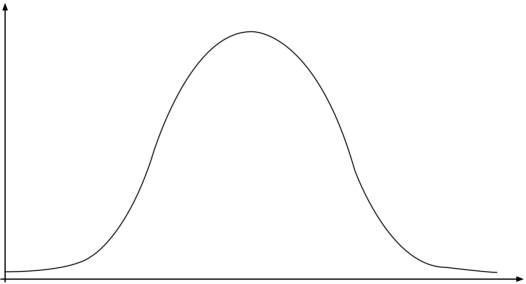
图5.13　函数f3（x）曲线

由上述讨论，可建立Logistic白化权函数。设

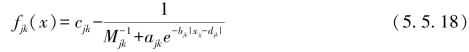
对fjk（x）求一阶导数，有

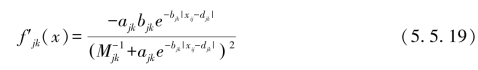
对fjk（x）求二阶导数，有

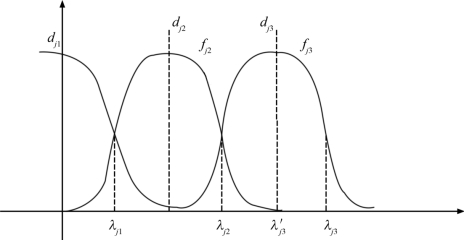
图5.14　Logistic白化权函数拐点示意图

其中

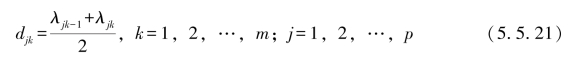
因为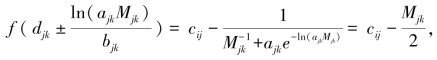即拐点的函数值为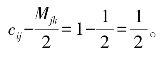不妨设白化权函数fjk右侧拐点与fjk＋1左侧拐点重合，拐点横坐标均为白化值λk（k＝1，2，…，m－1）。由于

fjk＋1（x）曲线右拐点，即第k类中心点的右侧拐点为

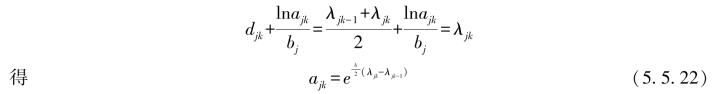
这里1≤k≤m－1。(www.daowen.com)

fjk＋1（x）曲线左拐点，即第k＋1类中心点的左侧拐点为

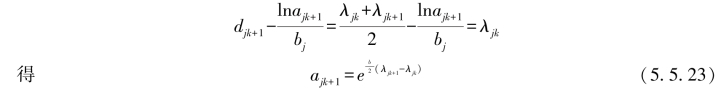
这里1≤k≤m－1。由此可得白化权函数fjk中，这里1≤k≤m。

5.5.2.3　聚类算法分类效用分析

分类效用最初是由M.Gluck和J.Corter于1985年提出的“类别好”的量度。它尝试最大化同一类别中的两个对象具有共同属性值的概率，以及来自不同类别的对象具有不同属性值的概率。它是具备给定类别结构知识的观察者给不具备类别结构知识的观察者提供的一种预测增长优势的规范性的信息理论度量。从这一层面考虑，分类度量的动机与决策树学习中使用的信息增益度量相似。分类效用CU被用来评判聚类结果的好坏。CU值较小表明聚类较差，CU值较大表明聚类较好。CU定义为

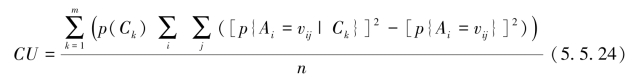
式中Ai表示第i个属性，vij是属性Ai的第j个属性值，Ck是第k个聚类，m代表聚类的数目。p（Ck）代表聚类Ck的数据所占的比例。式子的意义在于首先测量Ai＝vij时，在整个数据库中的概率为p｛Ai＝v ij｝，p｛Ai＝vij｜Ck｝是当样本在聚类Ck中的条件概率。

5.5.2.4　Logistic白化权函数的模型参数假设

为了方便起见，不妨设λj0＝－λj1，即dj1＝0。fjk函数曲线的右拐点横坐标为

由白化权函数的实际意义，可以进行下面的讨论和假设：

（1）由于0＜f（x）＜1，且不妨设cjk和Mjk恒为常数1，每个白化权函数都介于0和1之间，即0≤fjk（x）≤1，这样能保证每点x处各白化权函数之和接近于1。

（2）参数bj讨论。

对于同一个评价对象，属于各类的权重之和为1。由于Logistic白化权函数fjk曲线的拐点斜率为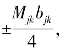所以不妨假设同一评价指标白化权函数的bjk都等于同一个常数，即bjk＝bj，这样的白化权函数设计使得各类的边界形状及特征相似，并能使得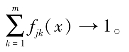

对于白化权函数设计时必须满足下列条件：

Ⅰ.如果设计白化权函数精度误差为εf，则要求必满足

Ⅱ.为白化权函数的最值接近于1，白化权函数拐点的斜率的绝对值大于白化权函数的最值点与拐点的连线斜率绝对值，即

Ⅲ.如果白化权函数拐点斜率的绝对值过大，使得白化权函数取值非0即1，其斜率阈值根据实际问题而定。如图5.15所示。

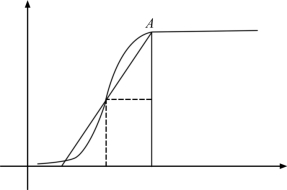
图5.15　拐点斜率示意图

综上讨论可得参数bj应满足下列条件：

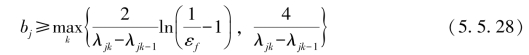
由Logistic白化权函数所建立的聚类算法称为Logistic白化权聚类算法。

在满足式（5.5.28）的情况下，进行聚类算法分类效用分析，选取使CU值最大的参数bj的值。

5.5.2.5　Logistic白化权函数特点

由上述推论和假设得到任何一个样本，有如下特点：

Ⅰ.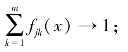

Ⅱ.在类临界点处，属于相邻两类的权重分别为50%。

5.5.2.6　Logistic白化权聚类算法步骤

算法：Logistic白化权聚类算法。

输入：聚类对象样本数据，聚类参数m，b。

输出：带有集群标签的数据对象。

步骤：

（1）数据清洗和标准化处理。

（2）差分法确定聚类白化值。

（3）标定聚类权。

（4）确定类白化函数。

（5）灰色聚类系数矩阵。

（6）给出带有集群标签的数据对象。

（7）停止。

这里参数b可以通过分类效用分析法聚类结果分析而进一步的优化。

5.5.2.7　Logistic白化权聚类算法优势

将白化权函数改进成Logistic白化权函数后，可使得聚类算法具有以下优势：

（1）在灰色系统中，一个评价对象完全属于某一灰类或完全不属于某一灰类都是不确切的，Logistic白化权聚类算法中，避免白化权函数值为0的情况。

（2）在灰色系统中，各灰类完全不相关的情况并不存在。Logistic白化权函数考虑了各类之间的影响，针对每一个评价对象，均有各类白化权函数值存在，避免丢失相互影响的有用信息。

（3）Logistic白化权聚类算法，评价对象通过白化权函数的映射，使得各类的边界更加清晰。

（4）白化权函数是初等函数，改变了以往白化权函数是分段函数的问题，便于理论分析，降低传统函数公式的理解难度，便于研究白化权函数的曲线特征，根据实际问题调整曲线参数，提高聚类精度。

（5）传统白化权聚类算法中，若灰类区间过长会使得评价对象在分类临界值，即白化值附近的权重变小，导致分类不准确。而在Logistic白化权聚类算法中，不论各类区间长短，在分类临界值，即白化值处，Logistic白化权函数曲线特征不发生变化。避免了由于不同类区间长度差异造成的结果不公正性。