灰色聚类是灰色系统理论中的决策方法之一。它是对多维度的灰色系统进行评估的一种方法，以生成灰数的白化函数为基础，按不同灰类将聚类对象对于不同聚类指标所拥有的白化数进行总结，从而判断聚类对象属于哪一个灰类。

5.5.1.1　灰色聚类分析方法

（1）建立评价矩阵

设n个聚类数据样本为x1，x2，…，xn，每个数据有p个评价指标，即

建立评估样本矩阵X，即样本矩阵为

其中xij为第i个样本第j个指标的样本值，i∈｛1，2，…，n｝为评价对象，j∈｛1，2，…，p｝为评价指标。

（2）确定灰类及白化值

引入几个概念。

灰类：是指评价指标最终聚类所属类别。

灰数：是指只知道其大致范围但是不知其准确值的数，在实际中，灰数指在某个数集内或某个区间内取值的不确定的数。

灰数白化值：设ai为区间I中的数，若a在I中取值，则称ai为a的一个可能的白化值。

通常采用概率统计方法，分析评价指标数据的累积频率，按一定的需求标准，指定若干个不同累积频率所对应的数值作为各灰类的白化值，记作λ1，λ2，…，λm，其中m为聚类评判灰类数。

（3）确定评价灰类的白化权函数f（x）

白化权函数被用来描述一个灰数的“偏爱”，即灰数取值范围内不同数值的“偏爱”程度。

研究中常使用的白化权函数有4种基本形式，下面分别介绍这4种基本形式，即典型白化权函数、下限测度白化权函数、适中测度白化权函数及上限测度白化权函数，如图5.9所示。

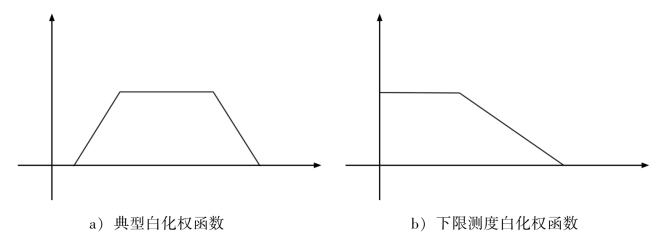
典型白化权函数：如图5.9（a）所示，4个转折点的横坐标分别为x（1），x（2），x（3），x（4），则典型白化权函数设为：

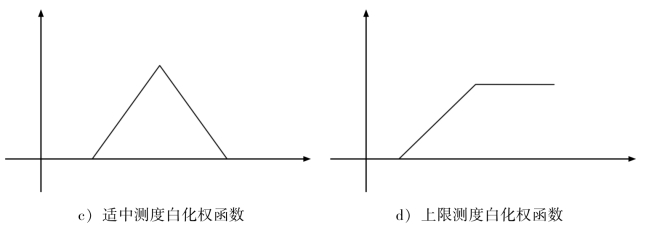
图5.9　常用4种白化权函数图示

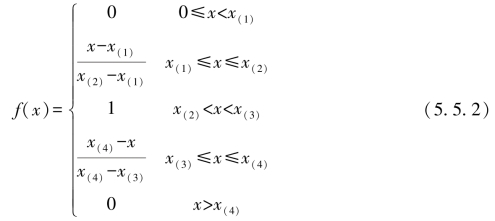
下限测度白化权函数：如图5.9（b）所示，两个转折点的横坐标分别为x（1），x（2），下限测度白化权函数设为：

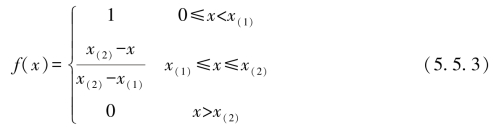
适中测度白化权函数：如图5.9（c）所示，三个转折点的横坐标分别为x（1），x（2），x（3），适中测度白化权函数设为：

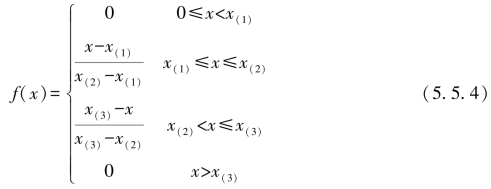
上限测度白化权函数：如图5.9（c）所示，三个转折点的横坐标分别为x（1），x（2），x（3），上限测度白化权函数设为：

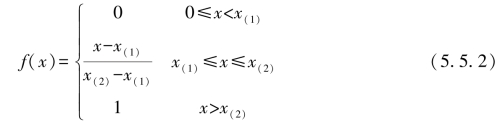
（4）求聚类权重

聚类评判灰类有m个，k∈｛1，2，…，m｝为评价灰类。则聚类权重ηjk根据下式确定：

(www.daowen.com)

式中ηjk为第j个指标关于评价第k灰类的权；λjk为第j项评价指标对第k灰类的白化值。

（5）求灰色聚类系数矩阵

设

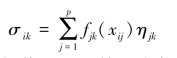
其中fjk（xij）是样本xi关于第j指标值xij属于第k个灰类的白化权。

σik综合反映第i个评价对象属于第k个灰类的“偏爱”程度，称σik为灰色聚类系数。

建立灰色聚类系数矩阵∑，即

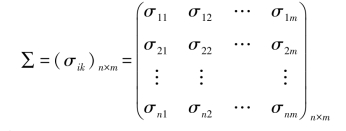
（6）确定样本灰类

若

则第i个聚类对象属于第m*个灰类。

5.5.1.2　灰色聚类步骤

算法：灰色聚类。

输入：聚类对象样本数据，聚类白化值。

输出：带有集群标签的数据对象。

步骤：

（1）数据清洗和标准化处理。

（2）给出聚类白化值。

（3）标定聚类权。

（4）确定灰类白化函数。

（5）求聚类系数。

（6）灰色聚类系数矩阵。

（7）给出带有集群标签的数据对象。

（8）停止。

5.5.1.3　传统灰色聚类算法存在的问题

白化权函数的选择是将信息数据定性分析定量化的关键，它的选取是灰色聚类的关键环节之一，是对一个灰数在取值范围内各个数值的偏重情况的描述，表示各评价数据在不同灰类中的可能性大小。白化权函数是研究者根据待评价对象的已知数据资料和信息确定，其关键是确定公式的转折点，转折点的选择是否正确直接反映函数选取的科学性，影响最终的决策结果。

传统白化权函数存在以下缺点：

（1）白化权函数fik只在相邻白化值之间取值，而在其他区域内，白化权函数取值为0，即只考虑相邻灰类之间的影响，因此会丢失很多有用的信息；

（2）由于不同灰类的区间长度差异很大，直边（梯形的腰）的斜率有很大差距，会使结果不具备应有的公正性。