DBSCAN算法基于一个事实：一个聚类可以由其中的任何核心对象唯一确定。等价可以表述为任一满足核心对象条件的数据对象a，数据库S中所有从a密度可达的数据对象所组成的集合构成了一个完整的聚类C，且a属于C。

DBSCAN是一个基于密度的聚类算法，基于密度的聚类是寻找被低密度区域分离的高密度区域。聚类是找出样本比较密集的部分，每一个密集部分就是一个类。基于密度的聚类的关键思想是：对于聚类中的每一个对象，在给定半径（Eps）的邻域中至少要包含最小数目（MinPts）个对象，即邻域的基数必须超过一个阈值。算法的具体聚类过程如下。

扫描整个数据集，找到任意一个核心点，对该核心点进行扩充。扩充的方法是寻找从该核心点出发的所有密度相连的数据点。遍历该核心点的邻域内的所有核心点（因为边界点是无法扩充的），寻找与这些数据点密度相连的点，直到没有可以扩充的数据点为止。最后聚类成的簇的边界节点都是非核心数据点。之后就是重新扫描数据集（不包括之前寻找到的簇中的任何数据点），寻找没有被聚类的核心点，

再重复上面的步骤，对该核心点进行扩充直到数据集中没有新的核心点为止。数据集中没有包含在任何簇中的数据点就构成异常点。

5.4.1.1　相关概念

（1）密度：空间中一点的密度为以该点为圆心，以Eps为半径的圆内包含样本点数目。

（2）Eps—邻域：给定对象半径Eps内的邻域称为该对象的Eps邻域，我们用NEps（a）表示点a的Eps—半径内的点集合，即

（3）核心对象（核心点）：如果一个对象的Eps—邻域内至少包含MinPts（最小包含点数）个样本点，则称其为核心对象。

（4）稠密区域内部的点样本：在半径Eps内含有超过MinPts数目的样本点，则该点为稠密区域内部的核心点，这些点都是在簇内的；

（5）稠密区域边缘上的点（边界点）：在半径Eps内样本点的数量小于MinPts，但是在核心点的邻域点。边界点不是核心点，但落在某个核心点的邻域内。

Ⅰ.对于任意的a，b∈S，如果b∈C并且a是从b基于密度可达的，那么a∈C；

Ⅱ.对于任意的a，b∈C，a和b是基于密度可连接的。

（6）直接密度可达：给定一个对象集合S，如果a在b的Eps邻域内，而b是一个核心对象，则称对象a从对象b出发时是直接密度可达的（directly density—reachable）。

（7）密度可达：如果存在一个对象链a1，a2，…，an，这里a1＝b，an＝a，对于ai∈S（1≤i≤n），ai＋1是从ai关于Eps和MinPts直接密度可达的，则对象a是从对象b关于Eps和MinPts密度可达的（density—reachable）。

（8）密度相连：如果存在对象0∈S，使对象a和b都是从O关于Eps和MinPts密度可达的，那么对象a到b是关于Eps和MinPts密度相连的（density－connected）。

（9）类：对于参数Eps和MinPts，一个类C是满足下面两个条件的S的非空子集：

（10）噪声：不属于任何一类的对象被认为是噪声。如图5.3和图4所示。

5.4.1.2　算法描述

DBSCAN以Eps和MinPts为输入参数来控制类的密度。其聚类过程基于以下事实：(www.daowen.com)

（1）给定满足核心对象的点a，从点a关于Eps和MinPts密度可达的所有对象组成的集合构成一个类，a属于该类；

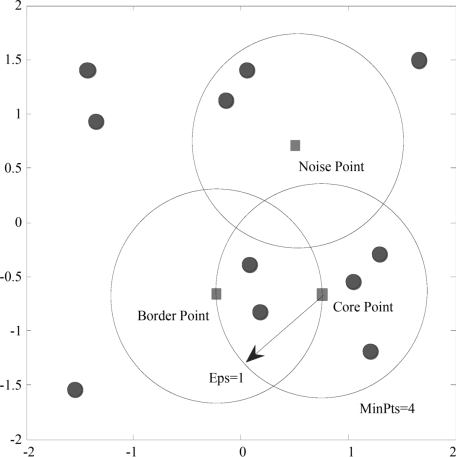
图5.3　核心点、边界点及噪声

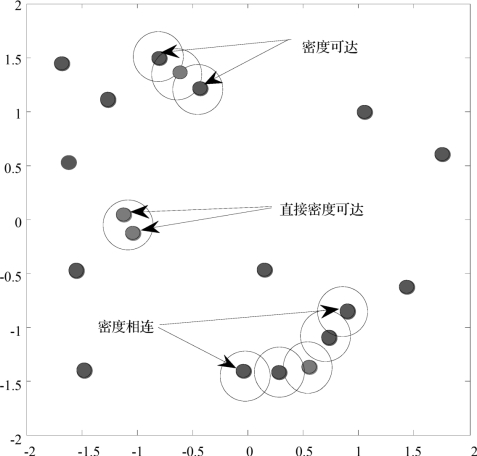
图5.4　“直接密度可达”“密度可达”和“密度相连”概念示意描述

（2）假定C是关于Eps和MinPts的一个类，a是类C中的一个核心对象，那么类C等价于从a关于Eps和MinPts密度可达的点的集合。基本思想是通过检查数据库中每一个点的Eps一邻域来寻找聚类。如果一个点a的Eps一邻域包含多于MinPts个点，则创建一个以a作为核心对象的新类。然后，反复寻找从这些核心对象直接密度可达的对象，这个过程可能涉及一些密度可达类的合并。当没有新的点可以被添加到任何类时，聚类过程结束。

DBSCAN算法描述：

算法：DBSCAN算法

输入：包含n个对象的数据库，半径Eps，最少数目MinPts；

输出：所有生成的簇，达到密度要求。

（1）repeat

（2）从数据库中抽出一个未处理的点；

（3）if抽出的点是核心点then找出所有从该点密度可达的对象，形成一个簇；

（4）else抽出的点是边缘点（非核心对象），跳出本次循环，寻找下一个点；

（5）until所有的点都被处理。

DBSCAN对用户定义的参数很敏感，细微的不同都可能导致差别很大的结果，而参数的选择无规律可循，只能靠经验确定。

5.4.1.3　优势和缺点

DBSCAN聚类算法优点：基于密度定义，相对抗噪声，能处理任意形状和大小的簇。

DBSCAN聚类算法缺点：当簇的密度变化太大时，会有麻烦；对于高维问题，密度定义是个比较麻烦的问题。