5.2.2.1　K－Medoid算法工作原理

K－Medoid算法，即K－中心聚类算法，是基于划分的聚类方法，基本思路是给定数据集，通过迭代的方式构造数据集的k个划分，一个划分代表一个簇。该方法事先随机选定k个实际对象x1，x2，…，xk来作为k个簇的初始中心点，即wi＝xi（i＝1，2，…，k），以此作为参照点，然后计算其余所有对象与各参照点的距离di（x）＝（x－wi）2（x∈S），即对象间的相异度，相异度越小，越相似，继而将剩余的每个对象分配到与其最相似的参照点所在的簇当中，生成初始k个簇，即簇C1，C2，…，Ck。

重复迭代尝试让每个代表对象都成为簇的实际中心点，比较各种中心点选择方案，取代价最小者为最佳。由此确定n个对象划分到k个簇的分配方案。而聚类结果的好坏则通过代价函数来计算，即对象与其簇的参照中心点之间的平均相异度。

聚类结果的质量用一个误差平方和SAD代价函数简称SAD来估计，即

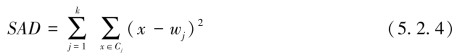
该函数评估了对象与其参照对象的平均相异度。

PAM算法是最早提出的基于划分的算法之一。PAM聚类算法的基本思想是选用簇中位置最中心的对象，试图对n个对象给出k个划分。代表对象也被称为是中心点，其他对象则被称为非代表对象。最初随机选择k个对象作为中心点，该算法反复地用非代表对象来代替代表对象，试图找出更好的中心点，以改进聚类的质量。在每次迭代中，所有可能“成对”的对象被分析，每个“成对”中的一个对象是中心点，而另一个是非代表对象。对可能的各种组合，估算聚类结果的质量。一个对象wj（j＝1，2，…，k）可以被与簇内各样本点的距离平方和最小的点所代替。在一次迭代中产生的最佳对象集合成为下次迭代的中心点，直至收敛。为了确定任一个非聚类代表对象是否可以替换当前一个聚类代表Q，这里Q，R是聚类代表，O，P是非聚类代表。需要根据以下四种情况对各非聚类代表对象P进行检查。见图5.1。

图5.1　非聚类代表对象P检查

图5.1（1）表示若对象O当前属于Q（所代表的聚类），且如果用P替换Q，作为新聚类代表，而O就更接近其他R，那么就将O归类到R（所代表的聚类）中；

图5.1（2）表示若对象O当前属于Q（所代表的聚类），且如果用P替换Q，作为新聚类代表，而O最接近P，那么就将O归类到P（所代表的聚类）中；

图5.1（3）表示若对象O当前属于R（所代表的聚类），且如果用P替换Q，作为新聚类代表，而O仍然最接近R，那么O归类不发生变化；

图5.1（4）表示若对象O当前属于R（所代表的聚类），且如果用P替换Q，作为新聚类代表，而O最接近P，那么就将O归类到P（所代表的聚类）中。(www.daowen.com)

每次对象重新归类，都会使得聚类误差平方和代价函数SAD发生变化，因此借助代价函数能够计算出聚类代表替换前后的方差变化。通过替换不合适的代表使距离方差发生变化的差值ΔSAD就构成了成本函数的输出。若整个输出成本为负值，那么就用P替换Q，以便能够减少实际的代价函数SAD。若整个输出成本为正值，那么就认为当前的Q，是可接受的，本次循环就无须变动。

5.2.2.2　PAM算法处理描述

算法：PAM算法。

输入：类的数目k和包含n个对象的数据库

输出：k个类簇集合

步骤：

（1）从n个数据对象任意选择k个对象作为初始聚类代表（聚类中心）；

（2）循环（3）到（6）

（3）依次计算其余各非聚类代表对象与这些聚类代表间的距离，并根据最小距离原则将各对象分配到离它最近的聚类代表所在的簇中；

（4）任意选择一个非中心对象P，计算其与中心对象Q，交换的成本函数ΔSAD；

（5）若ΔSAD为负值则P替换Q，构成新聚类的k个中心对象。

（6）每个聚类不再发生变化。