J.B.MacQueen在1967年提出的K－Means算法，是到目前为止用于科学和工业应用的诸多聚类算法中一种极有影响的技术。它是聚类方法中一个基本的划分方法，常常采用误差平方和代价函数（代价函数的意义是对异常信号的损失达到最小）SAD作为聚类准则函数，误差平方和代价函数SAD（Sun of Absolute Differences）为

SAD表示所有对象的平方误差总和，x表示所给定的数据对象，Ci（i＝1，2，…，k）分别代表k个类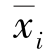，是簇Ci中数据对象的均值，即是簇Ci形成的新质心。

5.2.1.1　K－Means算法的工作原理

算法首先随机从数据集中选取k个数据对象作为初始聚类质心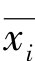（i＝1，2，…，k），然后计算各个样本到各聚类质心的距离，把样本归到离它最近的那个聚类质心所在的簇Ci（i＝1，2，…，k），即赋予样本x类标号为

这样把样本按赋予的类标号把样本集划分为k个类簇，计算新形成的每一个簇Ci中数据对象的平均值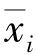，并以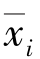为聚类更新质心进行重新划分k个类簇C1，C2，…，Ck，以此分下去。如果相邻两次的误差平方和代价函数SAD不变（或改变小于给定的阈值），即聚类质心没有任何变化，说明样本调整结束，聚类准则函数已经收敛。

本算法的一个特点是在每次迭代中都要考察每个样本的分类是否正确。若不正确，就要调整，在全部样本调整完后，再修改聚类质心，进入下一次迭代。如果在一次迭代算法中，所有的样本被正确分类，则不会有调整，聚类中心也不会有任何变化，这标志着已经收敛，因此算法结束。

K－Means均值聚类是基于质心的算法，质心通常代表的是一个簇中说包含对象的平均值。该算法先随机选取k的研究对象作为质心，计算剩余的每个对象离质心的距离，根据最近原则并将其划分到簇，然后重新计算各个簇的质心，这个过程反复进行多次，直到聚类准则函数收敛。该准则将使得聚类生成的结果簇既紧凑又独立。

5.2.1.2　算法描述

算法：K－Means。

输入：类的数目k和包含n个对象的数据库

输出：k个类簇集合

步骤：

（1）对于数据对象集，任意选取k个对象（i＝1，2，…，k）作为初始的类中心；

（2）根据类中对象的平均值，将每个对象重新赋给最相似的类；

（3）更新类的平均值，即更新后每个类中对象的平均值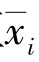（i＝1，2，…，k）；

（4）Repeat（2）和（3）；(www.daowen.com)

（5）直到不再发生变化。

SAD值依赖于的几何形状和位置。可以看出SAD值是对象和聚类质心的函数，数据对象集S给定的情况下SAD值取决于k个聚类质心。SAD值描述n个样本聚类成k个类时所产生的总的误差平方和。显然，若SAD值越大，说明误差越大，聚类结果越不好。因此，应该寻求使SAD值最小的聚类结果，即在误差平方和代价函数SAD值下的最优结果。这种聚类通常也称为最小方差划分。

5.2.1.3　K－Means均值聚类优势和存在的问题

K－Means算法的特点：采用两阶段反复循环过程算法，结束的条件是不再有数据元素被重新分配：

（1）指定聚类，即指定样本到某一个聚类，使得它与这个聚类中心的距离比它到其他聚类中心的距离要近。

（2）修改聚类中心。

K－Means聚类算法的优点主要集中在：

Ⅰ.算法快速、简单；

Ⅱ.对大数据集有较高的效率并且是可伸缩性的；

Ⅲ.时间复杂度近于线性，而且适合挖掘大规模数据集。

K－Means聚类算法存在的问题：

（1）在K－Means算法中k是事先给定的，这个k值的选定是非常难以估计的。很多时候，事先并不知道给定的数据集应该分成多少个类别才最合适。这也是KMeans算法的一个不足。有的算法是通过类的自动合并和分裂，得到较为合理的类型数目k，例如ISODATA算法。关于K－Means算法中聚类数目k值的确定，有研究者是根据方差分析理论，应用混合F统计量来确定最佳分类数，并应用了模糊划分熵来验证最佳分类数的正确性。

（2）在K－Means算法中，首先需要根据初始聚类中心来确定一个初始划分，然后对初始划分进行优化。这个初始聚类中心的选择对聚类结果有较大的影响，一旦初始值选择得不好，可能无法得到有效的聚类结果，这也成为K－Means算法的一个主要问题。对于该问题的解决，许多算法采用遗传算法（GA）进行初始化，以内部聚类准则函数作为评价指标。

（3）从K－Means算法框架可以看出，该算法需要不断地进行样本分类调整，不断地计算调整后的新的聚类质心，因此当数据量非常大时，算法的时间开销是非常大的。所以需要对算法的时间复杂度进行分析、改进，提高算法应用范围。目前有研究者从时间复杂度进行分析考虑，通过一定的相似性准则来去掉聚类质心的候选集。