4.6.8.1　依据SLIQ算法建立决策树分类器

（1）属性排序。输入有具有7个属性训练数据集D1。本数据集中的类标和属性取值采用的是0－1取值，即每个属性取值都是0和1，类标签为0和1两类。计算各属性的信息增益。如表4.1。

表4.1　属性信息增益

更新属性排序，即按从大到小的顺序排序。如表4.2。

表4.2　按增益信息从大到小的顺序排序

在每个内部结点寻找其最优分裂标准时，都需要对训练集按照该属性的取值进行排序，而排序是很浪费时间的操作。为此，SLIQ算法采用了预排序技术。所谓预排序，就是针对每个属性的取值，把所有的记录按照从小到大的顺序进行排序，以消除在决策树的每个结点对数据集进行的排序。具体实现时，需要为训练数据集的每个属性创建一个属性列表，为类别属性创建一个类别列表。

（2）SLIQ算法的广度优先策略，即输入样本后，按预先排列的属性顺序，一层一层的分裂属性，优先访问一层结点。

（3）设置节点分裂阈值。设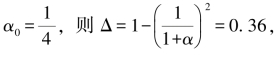叶节点的所含最大样本个数的属性的样本数与样本总数比为即节点当最大样本个数的属性的样本数与样本总数比小于0.8时，该节点分裂。为防止过度分类而使决策树过大的现象出现设样本总数小于8节点停止分裂。

（4）建立分类决策树。得到十个叶节点，依据每个叶节点的α值，确定该节点的判别类别。其各叶节点的路径如表。计算对数据集D1的判别精度为0.8398。如表4.3。

表4.3　分类决策树各叶节点的路

续表

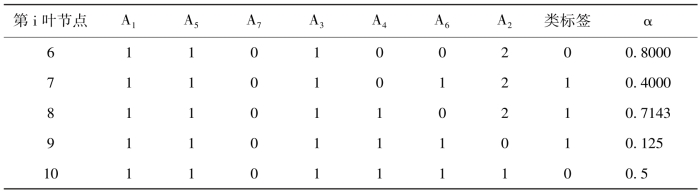
表中出现的α值过大的现象是该节点的样本总数过小而停止分裂，由于样本总数较小，所以对决策树的分类精度影响不大。该节点的分类标签取值为频率大的类别，当各类频率相同时取0类标签。

（5）输入数据集D2。运用D2中带类标签的数据子集I1对判别精度进行打分，该决策树的判别精度为0.7835。

4.6.8.2　依据IARF算法建立随机森林分类器

（1）属性排序。随机选取5个排序队列（属性），并设属性排序

(www.daowen.com)

为i1，i2，i3，i4，i5，i6，i7，所对应构建的子决策树分别为分类器1、分类器2、分类器3、分类器4及分类器5，可得属性排序队列表4.4。

表4.4　属性排序队列

（2）用训练集D1构建增量自适应随机森林分类器，同时计算各子分类器的判别精度，分别为a1（0），a2（0），…，a7（0），称其为初始精度。如表4.5。

表4.5　IARF分类器初始精度

（3）对数据流时间标签为t的输入数据集D2各样本判别其类别，同时对样本的数据标签取值为以类别精度为权值进行加权投票的结果。计算有其带标签的数据子集I1计算该各子分类器的判别精度为a1（t），a2（t），…，a7（t），同时计算IARF分类器加权投票后，给出数据集D2的类标签。如表4.6。

表4.6　IARF分类器分类精度

IARF分类器分类精度下降，说明数据流已概念漂移，数据信息特征已经变化，更新IARF分类器，对精度小于0.75的分类器4和分类器5进行“砍伐”，以数据集I1为训练集，构建两棵决策树，如表4.7。

表4.7　新建分类器叶节点路径及其分类精度

更新IARF分类器如表4.8。

表4.8　更新IARF分类器叶节点路径及其分类精度

随着数据流的概念漂移，自适应的更新随机森林决策树，已达到提高分类精度。

通过仿真可以看到以下几个问题。

（1）由表4.5可以看出，IARF决策树分类精度由于采用加权投票的方式判断，并不比SLIQ分类器的判别精度低，随着数据流的概念漂移，SLIQ分类器的判别精度会变得越来越低，而IARF决策树的自适应更新功能，使得分类精度会保持在某一个范围内，当超出该范围会自动更新随机森林；

（2）分类精度具有可控性，可通过调整节点分类阈值和随机森林中的决策树个数以及随机森林更新条件的设置等来控制精度；

（3）IARF算法简单，可操作性较强，适用范围广。