对于一个样本向量x进行分类，实际上是通过把x带入到f（x）＝wTx＋b，算出结果，然后根据其正负号来进行类别划分的。而前面的推导中我们得到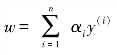x（i），因此分类函数为

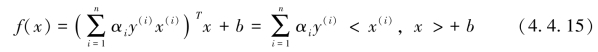
这里形式的有趣之处在于，对于新点x的预测，只需要计算它与训练数据点的内积即可（〈·，·〉表示向量内积），这一点至关重要。此外，所谓支持向量也在这里显示出来，事实上，所有非支持向量所对应的系数向量α都是等于0的，因此对于新点的内积计算实际上只要针对少量的“支持向量”而不是所有的训练数据即可。为什么非支持向量对应的α等于0，直观上来理解的话，就是这些“后方”的点——正如我们之前分析过的一样，对超平面是没有影响的，由于分类完全有超平面决定，所以这些无关的点并不会参与分类问题的计算，因而也就不会产生任何影响了。

先考虑我们特征空间的隐式映射——核函数。

对于非线性的情况，SVM的处理方法是选择一个核函数k〈·，·〉，通过将数据映射到高维空间，来解决在原始空间中线性不可分的问题。由于核函数的优良品质，这样的非线性扩展在计算量上并没有比原来复杂多少，这一点是非常难得的。现实世界复杂的应用需要有比线性函数更富有表达能力的假设空间，也就是说，目标概念通常不能由给定属性的简单线性函数组合产生，而是应该一般地寻找待研究数据的更为一般化的抽象特征。

在线性不可分的情况下，支持向量机通过某种事先选择的非线性映射（核函数）将输入变量映射到一个高维属性空间，在这个空间中构造最优分类超平面。我们使用SVM进行数据集分类工作，首先是同预先选定的一些非线性映射将输入空间映射到高维属性空间，使得在高维属性空间中有可能使训练数据实现超平面的分割，避免了在原输入空间中进行非线性曲面分割计算。SVM数据集形成的分类函数具有这样的性质：它是一组以支持向量为参数的非线性函数的线性组合，因此分类函数的表达式仅和支持向量的数量有关，而独立于空间的维度，在处理高维输入空间的分类时，这种方法尤其有效。

再来分析核函数如何处理非线性数据。

举个例子来说，如图4.3所示的两类数据，分别分布为两个曲线的形状，这样的数据本身就是线性不可分的，此时咱们该如何把这两类数据分开。(www.daowen.com)

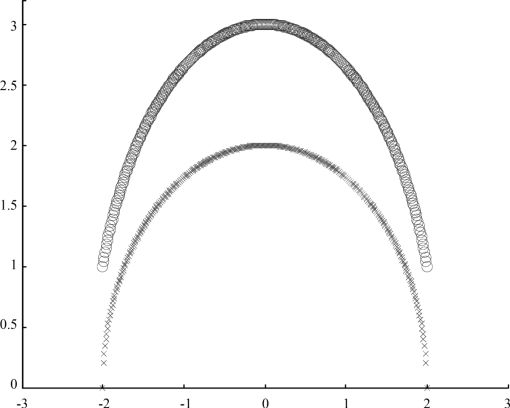
图4.3　非线性数据

事实上，图4.3所述的这个数据集，是用两条曲线加上了少量的噪声生成得到的，所以，一个理想的分界应该是一个曲线而不是一条线（超平面）。如果用x＝（x1，x2）来表示这个二维平面的两个坐标的话，我们知道一条二次曲线的方程可以写作这样的形式：

如果我们构造另外一个五维的空间，其中五个坐标的值分别为显然，上面的方程在新的坐标系下可以写作

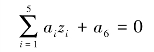
关于新的坐标z＝（z1，z2，…，z5），这正是一个超平面方程，也就是说，如果我们做一个映射φ：R2→R5，将x＝（x1，x2）按照规则φ映射为z＝（z1，z2，…，z5），那么在新的空间中原来的数据将变成线性可分的，从而使用之前我们推导的线性分类算法就可以进行处理了。这正是核方法处理非线性问题的基本思想。