4.4.2.1　分类标准

这里我们考虑的是一个两类的分类问题，数据点用x来表示，这是一个n维列向量，类标签用y来表示，可以取1或者－1，分别代表两个不同的类。一个线性分类器的学习目标就是要在n维的数据空间中找到一个分类超平面，其方程可以表示为

w是n维列向量。上面给出了线性分类的定义描述，为何用y取1或者－1来表示两个不同的类别，其实，这个1或者－1的分类标准起源于Logistic回归，为了完整和过渡的自然性，下面介绍一下Logistic回归。

4.4.2.2　Logistic回归

Logistic回归目的是从特征学习出一个0／1分类模型，而这个模型是将特性的线性组合作为自变量，由于自变量的取值范围是负无穷到正无穷。因此使用Logistic函数（或称作Sigmoid函数）将自变量映射到（0，1）上，映射后的值被认为是属于y＝1的概率。

形式化表示就是假设函数

其中x是p维特征向量，函数f就是Logistic函数。函数g（z）＝的图象见图4.1。

而Logistic函数值就是特征属于y＝1的概率，即

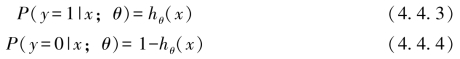
当我们要判别一个新的具有特征向量的样本所属类别，若hθ（x）＝g（θTx）值大于0.5就是y＝1的类，反之属于y＝0类。

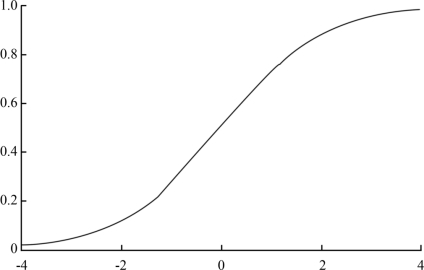
图4.1　Logistic函数曲线图

再审视一下hθ（x），发现hθ（x）只和θTx有关（θTx＞0），那么g（z）只不过是用来映射的，真实的类别决定权还在θTx。还有当θTx≫0时，hθ（x）＝1，QTx≪0时hθ（x）＝0。如果我们只从θTx出发，希望模型达到的目标无非就是让训练数据中y＝1的特征θTx≫0，而是y＝0的特征θTx≪0。Logistic回归就是要学习得到θ，使得正例的特征远大于0，负例的特征远小于0，强调在全部训练实例上达到这个目标。

4.4.2.3　假设函数形式化表示改进

假设函数形式化表示就是对类标签y用y＝－1和y＝1替换在Logistic回归中使用的y＝0和y＝1，同时将θ替换成w和b，即对于θTx＝θ0＋θ1x1＋θ2x2＋…＋θpxp（其中认为x0＝1）。

令θ0＝b，w＝（w1，w2，…，wp）T＝（θ1，θ2，…，θp）T，则θTx＝wTx＋b，故

也就是说，除了类标签y由y＝0变为y＝－1，与Logistic回归的形式化表示没区别。假设函数变为

上面提到过我们分类只需考虑θTx的正负问题，而不用关心g（z），因此我们这里将g（z）做一个简化，将其简单映射到y＝－1和y＝1上。映射关系如下：

即形式化表示假设函数即为

(www.daowen.com)

4.4.2.4　线性分类的一个例子

下面举个简单的例子，一个二维平面（一个超平面，在二维空间中的例子就是一条直线），如图4.2所示，平面上有两种不同的点，分别用两种不同几何形状表示，实线表示一个可行的超平面。

从图4.2中我们可以看出，这条实线把星符号和三角符号的点分开来了。而这条实线就是我们上面所说的超平面，也就是说，这个所谓的超平面的的确确把这两种不同符号的数据点分隔开来，在超平面一边的数据点所对应的y全是－1，而在另一边全是1。

接着，我们可以令分类函数

显然，如果f（x）＝0，那么x是位于超平面上的点。我们不妨要求对于所有满足f（x）＜0的点，其对应y＝－1，而f（x）＞0则对应y＝1的数据点。

为求图中超平面（wT＋b）＝0，求满足y（i）（wTx（i）＋b）≥1（i＝1，2，…，n）条件的w，b。设（wT＋b）＝1和（wT＋b）＝－1为边缘超平面，不同两类的样本被超平面隔在两侧，如图4.2，即y（i）＝1的样本点为满足wTx（i）＋b≥1；y（i）＝－1的为样本点满足wTx（i）＋b≤－1。

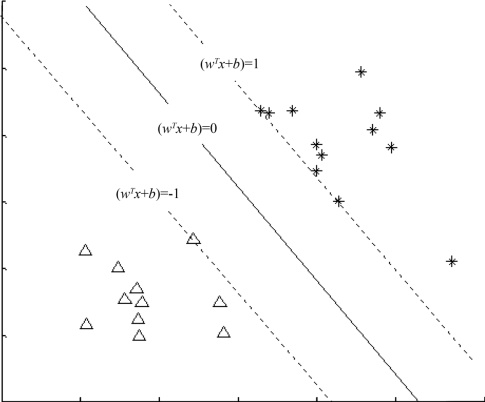
图4.2　超平面示意图

超平面方程中的w称为斜率向量；超平面方程中的b称为截距向量。两边缘超平面的距离越大分类精度越好。

分别取两边缘超平面的点x1和x2，即满足

且设两点连线与超平面垂直，称其为分离间隔。即两式相减得

不妨设x1≠x2，即超平面存在，则‖x1－x2‖＝

由上述分析，求超平面的问题即化为约束条件凸线性规划

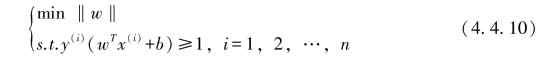
的求解问题。这里x（i）为第i的样本点的指标向量。

当然，有些时候数据并不是线性可分的，这个时候满足这样条件的超平面就根本不存在，这里先从最简单的情形开始推导，就假设数据都是线性可分的，亦即这样的超平面是存在的。

引入拉格朗日乘子α，建立拉格朗日函数

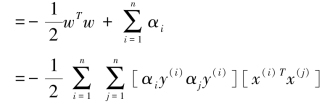
从上面的最后一个式子，我们可以看出，此时的拉格朗日函数只包含了一个向量，那就是α，求L（w，b，α）对α的极小问题，即是关于对偶问题的最优化问题。