贝叶斯分类是统计学分类方法，它是一类利用概率统计知识进行分类的算法。在许多场合，朴素贝叶斯（NB）分类算法可以与决策树和神经网络分类算法相媲美，该算法能运用到大型数据库中且方法简单、分类准确率高、速度快。由于贝叶斯定理假设一个属性值对给定类的影响独立于其他属性的值，而此假设在实际情况中经常是不成立的，因此其分类准确率可能会下降。为此，就出现了许多降低独立性假设的贝叶斯分类算法，如TAN算法。

4.3.2.1　朴素贝叶斯分类模型

假设样本空间有m个类别｛C1，C2，…，Cm｝，数据集有p个属性，A1，A2，…，Ap给定一未知类别的样本X＝（x1，x2，…，xp），其中xi表示第i个属性的取值，即xi∈Ai，则可用贝叶斯公式计算样本X＝（x1，x2，…，xp）属于类别Ci（1≤i≤m）的概率。由贝叶斯公式，有

即要得到P（Ci｜X）的值关键要计算P（X｜Ci）和P（Ci）。令C（X）为X所属的类别标签，由贝叶斯分类准则，如果对于任意i≠j都有P（Ci｜X）＞P（Cj｜X）成立，则把未知类别的样本X指派给类别Ci，贝叶斯分类器的计算模型为

由朴素贝叶斯分类器的属性独立性假设，假设各属性Ak（k＝1，2，…，p）间相互类条件独立，则

于是上式被修改为

P（Ci）为先验概率，可通过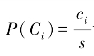计算得到，其中ci是属于类别Ci的训练样本的个数，s是训练样本的总数。若属性Ak是离散的，则概率可由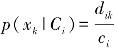计算得到，其中dik是训练样本集合中属于类Ci并且属性Ak取值为xk的样本个数，ci是属于类Ci的训练样本的个数。

4.3.2.2　朴素贝叶斯分类模型的算法描述

（1）对训练样本数据集和测试样本数据集进行离散化处理和缺失值处理；

（2）扫描训练样本数据集，分别统计训练集中类别Ci的个数ci和属于类别Ci的样本中属性Ak取值为xk的实例样本个数dik，构成统计表；(www.daowen.com)

（3）计算先验概率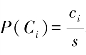和条件概率P（xk｜Ci）＝P（Ak＝xk｜Ci）＝构成概率表；

（4）构建分类模型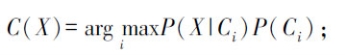

（5）扫描待分类的样本数据集，调用已得到的统计表、概率表以及构建好的分类准则，得出分类结果。

4.3.2.3　朴素贝叶斯分类器的优缺点

朴素贝叶斯分类算法有诸多优点：逻辑简单、易于实现、分类过程中算法的时间空间开销比较小；算法比较稳定、分类性能对于具有不同数据特点的数据集合其差别不大，即具有比较好的健壮性等优点。

尽管在实际情况中难以满足朴素贝叶斯模型的属性类条件独立性假定，但它分类预测效果在大多数情况下仍比较精确。原因有如下几个：要估计的参数比较少，从而加强了估计的稳定性；虽然概率估计是有偏的，但人们大多关心的不是它的绝对值，而是它的排列次序，因此有偏的概率估计在某些情况下可能并不重要；现实中很多时候已经对数据进行了预处理，比如对变量进行了筛选，可能已经去掉了高度相关的量等。除了分类性能很好外，贝叶斯分类模型还具有形式简单、可扩展性很强和可理解性很好等优点。

朴素贝叶斯分类器的缺点是属性间类条件独立的这个假定，而很多实际问题中这个独立性假设并不成立，如果在属性间存在相关性的实际问题中忽视这一点，会导致分类效果下降。

朴素贝叶斯分类模型虽然在某些不满足独立性假设的情况下分类效果不好，但是大量研究表明可以通过各种改进方法来提高朴素贝叶斯分类器的性能。朴素贝叶斯分类器的改进方法主要有两类：一类是弱化属性的类条件独立性假设，在朴素贝叶斯分类器的基础上构建属性间的相关性，如构建相关性度量公式，增加属性间可能存在的依赖关系；另一类是构建新的样本属性集，期望在新的属性集中，属性间存在较好的类条件独立关系。