集中趋势只是数据分布的特征之一，数据分布的另一个特征是数据的离散趋势，也称为离中趋势，它反映的是各变量值之间的差异程度。

离散趋势是一种差异分析。我们知道集中趋势是对数据水平的一个概括性度量，它能否代表一组数据，取决于该组数据的离散水平。数据的离散程度越小，说明数据之间的差别小，所有的数据都靠近集中趋势测度值，此时集中趋势测量值对该组数据的代表性就好。数据的离散程度越大，其集中趋势的代表性就越差。离散趋势测量的作用可归纳为两点，一个是衡量集中趋势的代表性，另一个是反映现象发展均衡与否。

离散趋势有多种测量方法，每一种方法的选择，可根据数据类型及集中趋势测度值的不同来决定。

2.3.3.1　非数值型数据离散趋势测量

（1）定类尺度

我们知道众数是定类尺度集中趋势的唯一测度方法。所以，衡量定类尺度集中趋势的代表性，其离散趋势测量方法也只有一种，那就是异众比率。

异众比率是非众数组的频数占总频数的比重，一般用Vr，即

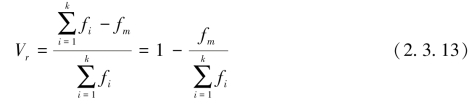
式中fm为众数组频数。

异众比率主要用于众数对一组数据代表性的评价，无论是什么类型的数据只要计算众数，其众数代表性的评价就必须用异众比率，也就是说，异众比率既适宜定类数据离散趋势的测量，也适宜定序数据及数值型数据离散趋势的测度。异众比率取值范围介于0～1之间，其取值越大，说明众数组的频数占总频数的比重越小，众数的代表性就越差，表明数据分布不存在显著集中的态势。异众比率越小，说明众数组的频数占总频数的比重越大，众数的代表性就越好。

（2）定序尺度

基于计量尺度描述方法向下兼容的性质，定序尺度离散趋势的测度方法有两种，分别是四分位差和异众比率。所谓四分位差是指一组数据的第3个四分位数与第1个四分位数的差值，用QD表示。

当我们以中位数描述定序尺度的集中趋势，反映中位数对定序数据代表性的高低，则需采用四分位差测量离散趋势；倘若用众数测度定序尺度的集中趋势，则计算异众比率，测量离散趋势。

四分位数是一组数据排序后，用3个点将数据分成相等的四个部分，每一部分占观察值总数的25%。其中第1个25%数据点称为第1个四分位数，一般用Q1表示；第3个25%数据点，即75%数据处称为第3个四分位数，一般用Q3表示。很显然第2个25%数据点是中位数Me。用图形表示如下：

图2.3　四分位数

四分位差的计算公式：QD＝Q3－Q1

从图2.3可以看出，四分位差描述了距中位数两侧共50%数据的离散程度，其数值越大，说明50%数据离中位数的距离也越大，中位数的代表性就差。四分位差越小，说明50%数据集中在中位数两侧，则中位数的代表性好。四分位差不受极端值的影响。

四分位差主要用于定序尺度的离散程度，当然，数值型数据也可计算四分位差。

对于定序尺度计算四分位差，首先需将非数值型的定序尺度数值化，比如将非常满意设为1，满意为2，一般为3等。求出Q1和Q3的位置，并用向上累计频数确定Q1和Q3所对应的变量值，最后求出QD。例如，计算表2.8中数据的四分位差。

表2.8　满意量化统计表

先将满意度的5个层次分别用1、2、3、4、5代表，见表2.8。Q3的位置＝0.75×40＝30，即第30个人的态度是Q3，Q1的位置＝0.25×40＝10，即第10人的态度是Q1。

运用向上累计频数得知，第30个人在第2组，其对产品的态度是满意，用2表示。第10个人对产品的态度也在第2组，其态度值是满意，也用2表示。根据公式四分位差为

说明用中位数满意反映40个人对产品的态度其代表性极高。

2.3.3.2　数值型数据离散趋势测量

数值型数据离散趋势的测量方法有多种，有反映平均数代表性的全距、平均差、方差与标准差、离散系数；还有反映众数代表性的异众比率和衡量中位数代表性的四分位差。

（1）全距

全距是一组数据最大值与最小值的差值，用R表示。计算公式是：

全距是描述数值型数据离散趋势的最简单的一种计算方法。但由于没有充分利用数据的全部信息，同时易受极端值的影响。所以往往不能全面准确地反映数据的分散程度。全距只适宜在数据分布均匀时采用。

（2）平均差

平均差是指各变量值与平均数离差绝对值的平均数。用A.D.表示。计算公式为

①未分组资料：

②分组资料：

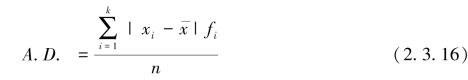
对于未分组资料，是采用简单平均法计算的，对于分组资料，则采用加权平均法计算。例如，根据某公司雇员周薪数据表信息，计算雇员周薪的平均差，见表2.9。

表2.9　某公司雇员周薪数据统计表

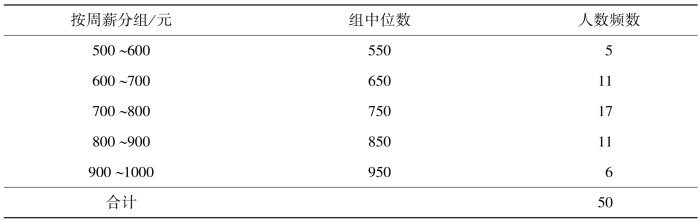
已知雇员周薪的平均数为754元，雇员周薪平均差为

平均差是根据全部数据计算的，能比全距和四分位差更好地反映数据的离散趋势。但平均差在计算过程中为了避免离差之和等于0，采取离差绝对值的形式，这给平均差的数学处理带来了麻烦，因而平均差在实践运用较少。

（3）方差与标准差

为了克服平均差的缺陷，考虑把离差的绝对值换成离差平方，再计算离差的均值，即为方差或标准差。这两种方法是数值型数据离散趋势测度最常用的方法。

①方差

方差是各变量值与平均数离差平方的均值。根据资料不同方差有不同计算形式。

Ⅰ.未分组资料

设一个总体有N个变量值，总体方差用σ2表示，则总体方差的计算公式为

对于一个包含n个变量值的样本，样本方差用S2表示，则样本方差的计算公式为

总体方差描述的是总体分布的差异特征，而样本方差说明的是从总体中抽出的样本的差异情况。从计算公式可以看出两者不仅计算范围不同，分母也有些不同。总体方差的分母是总体容量，样本方差的分母是样本容量减1，这在统计学中称为少一个自由度，且样本方差S2是总体方差σ2的无偏估计。

Ⅱ.分组资料

总体方差的计算公式为

例如，某会计师事务所今年新招聘了5名见习会计，5个人第一个月的收入（单位：元）分别为：1 200、1 500、1 400、1 300、1 800，计算方差。

所给的计算资料未经分组。分析题意，新雇用的5名见习会计是总体，所以，该计算属于求总体方差问题。先算得总体均值为

可得总体方差为

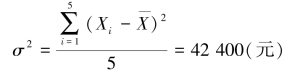
再如，根据某公司雇员周薪数据统计表2.9的信息，计算雇员周薪的方差。由样本加权平均数公式，先求出样本均值

将其代入样本方差公式可得

同其他离散趋势测量值一样，方差可用于比较两组或多组变量值的离散程度，也可用于平均数代表性的比较。

在上例中，5名新雇用见习会计第1个月收入的方差是42 400，倘若另一家会计师事务所，今年新雇用见习会计第1个月收入的均值也是1 440元，但方差是50 000，我们就可以得出这样的结论：第1家会计师事务所新雇用见习会计收入的离散程度低于另一家；与另一家相比第1家新雇用见习会计收入均值的代表性要好一些。(www.daowen.com)

但是，方差也有缺陷，那就是计量单位是原有单位的平方，给数据解释带来困难。因此，人们更习惯于采用计量单位与原单位一致的标准差。

②标准差

标准差是方差的平方根，即变量值与平均数离差平方平均数的平方根，亦称均方差。

Ⅰ.未分组资料

总体标准差的计算公式为

样本标准差的计算公式为

Ⅱ.分组资料

总体标准差的计算公式为

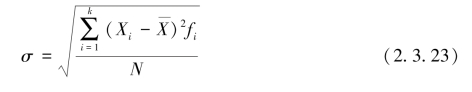
样本标准差的计算公式为

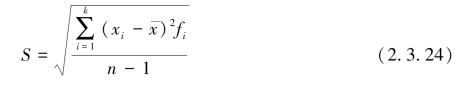
可以看出，标准差与方差同样都是测定数值型数据离散趋势的最好指标，标准差的计量单位与变量x的计量单位一致，与方差相比更易解释与说明研究问题的离散程度，但方差在公式推导与数据处理上比标准差更胜一筹。

③标准差的应用

标准差除具有上述用于反映均值代表性等作用以外，它还有助于了解一组数据是如何围绕均值而分布的；在数据呈正态分布的条件下，利用标准差可以确定某一变量值的相对位置。

Ⅰ.经验法则

经验法则是在正态分布的基础上建立的，人们有时将其称为正态法则。经验法则利用标准差所提供的信息，对位于均值两侧变量值出现的可能性给出3个具体的数值，只要记住这3个值，人们就可在免除烦琐数学计算的情况下，得到极有价值的信息。

经验法则是指当一组数据呈正态分布时，查表可得，大约有68%的变量值落在均值加减1倍标准差的范围内，约有95%的变量值落在均值加减2倍标准差的范围内，约有99.7%的变量值落在加减3倍标准差的范围内。

经验法则既适宜总体数据，也适宜样本数据，如果是总体数据，根据经验法则可得：

区间包括68%数据；

区间包括95%数据；

区间包括99.7%数据。

例如，假设18～25岁女性总体身高服从正态分布，身高的均值是159厘米，标准差6厘米，运用经验法则可得下面结论：

区间（153，165）包括68%数据；

区间（147，171）包括95%数据；

区间（138，177）包括99.7%数据。

Ⅱ.标准分

标准分是变量值与其均值的离差再除以标准差，也称为Z分数。

标准分描述了一个变量值与均值离差等同于多少倍标准差，运用标准分可以确定某一变量值的相对位置。比如某人年收入50 000元，这一收入在当地处于什么层次，利用标准分就可以解答。标准分可用于总体数据，也可用于样本数据。其计算公式为

总体数据

样本数据

例如，某求职者参加了两次智能测验，两次总体智能测验得分的分布均正态分布。第1次测验总体均值和标准差分别是80和4，该求职者得分84；第2次测验总体均值和标准差分别是60和7，该求职者得分70，而问求职者哪1次测验的成绩好？

该求职者两次测验得分不同，第1次得分比第2次多了14分，但并不能因此认定求职者第1次测验成绩的相对位次好于第2次。原因在于第1次测验的总体平均分比第2次高，而标准差却比第2次小，说明所有参加第一次测试的人都相对取得较好成绩，第2次则普遍较差。如果两次测验的总体均值和标准差均相等，认定84分好于70分才有意义。根据公式（2.3.25），计算标准分。

第一次：

第二次：

从计算结果看，求职者第2次测验的分数比总体平均数高了1.43倍的标准差，而第1次只比总体平均数高1倍标准差。所以该求职者第2次的成绩比第1次好。

（4）是非标志标准差

“是非标志”是品质标志，它有两种表现形式，通常用1表示具有某种属性的标志值，用0表示不具有某种属性的标志值。比如产品质量分为合格品与不合格品，人口按性别分为男与女等。

设总体容量为N，总体中具有某种属性的单位数为N1，不具有某种属性的单位数为N2，则

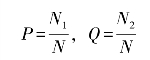
式中，P表示总体成数或总体比例，P＋Q＝1。

设样本容量为n，样本中具有某种属性的单位数为n1，不具有某种属性的单位数为n2，则

式中，p表示样本成数或总体比例，p＋q＝1。利用均值和标准差的计算公式，可得其标准差。

Ⅰ.总体“是非标志”的标准差。

首先计算总体“是非标志”的均值，可得

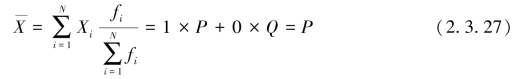
总体“是非标志”的标准差为

Ⅱ.样本是非标志的标准差。

样本是非标志的均值为

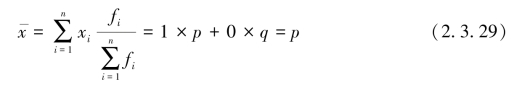
样本是非标志的标准差：

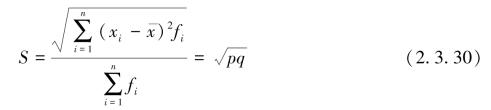
从上述计算可见，无论是总体还是样本，其“是非标志”的均值是具有某种标志的单位数所占的比重，而标准差则是具有某种标志的单位数所占比重和不具有某种标志单位数所占比重乘积的平方根。

（5）离散系数

前面介绍的全距、平均差、方差与标准差因其计算结果带有具体的计量单位，只适用于均值相同时两组数据离散趋势的比较。这就是说，比较两组数据分布的离散程度，不仅要看各自变量值差异的大小，还要考虑均值水平的高低。比如，甲组的均值15，标准差3；乙组均值20，标准差4时，我们不能仅凭甲组的标准差比乙组少1个单位，就说甲组的数据分布均匀、平均数的代表性好。因为乙组在标准差大于甲组的同时，其平均数也大于甲组。所以对两组或更多组数据的离散趋势进行比较时，当它们的均值不等、计量单位不同时，就需要用离散系数来测量离散趋势。

离散系数是离差值与平均数的比值，一般用百分数表示。离散系数有多种形式，最常用的是标准差系数，它是标准差与平均数的比值。

设Vσ表示总体标准差系数，则总体标准差系数的计算公式为

设VS表示样本标准差系数，则样本标准差系数的计算公式为