渐开线内齿轮副的啮合效率优化

在图10-1中，设外齿轮1为主动轮，内齿轮2为从动轮，啮合点Q的滑动速度可用下式表示：

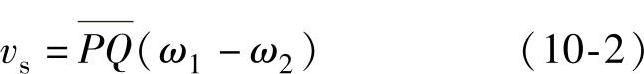
设法向载荷为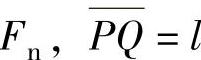，则在dt时间内的摩擦功为

dA=F_nμ_sv_sdt=F_nμ_sl（ω₁-ω₂）dt （10-3）

式中，μ_s为啮合齿轮之间的摩擦系数，可取μ_s=0.06～0.100。

在dt时间内接触点的移动距离dl为

dl=r_b1ω₁dt=r_b2ω₂dt

从而

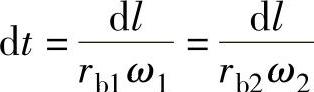
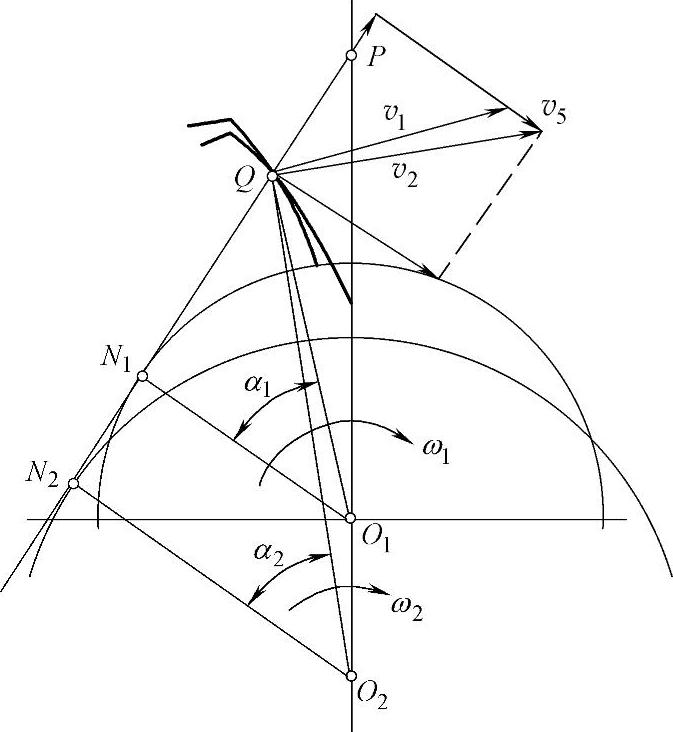
图10-1 内啮合齿轮副

把上式代入式（10-3）得

图10-2表示不发生过渡曲线干涉的少齿差内齿轮副的啮合状态。这时啮合角α′比外齿轮齿顶压力角α_a1大，A点为啮合起点，B点为啮合终点，因此，只在节点的一侧进行啮合，又称节点外啮合。图10-3表示1＜ε_α＜2时的接触点轨迹。根据式（10-4），在一齿啮合期间的摩擦功A为

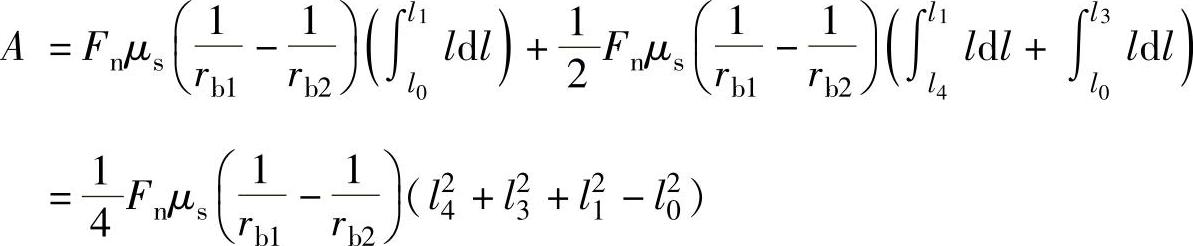
由图10-3可知，式中p_b——基节，l₃=l₁-p_b，l₄=l₀+p_b。

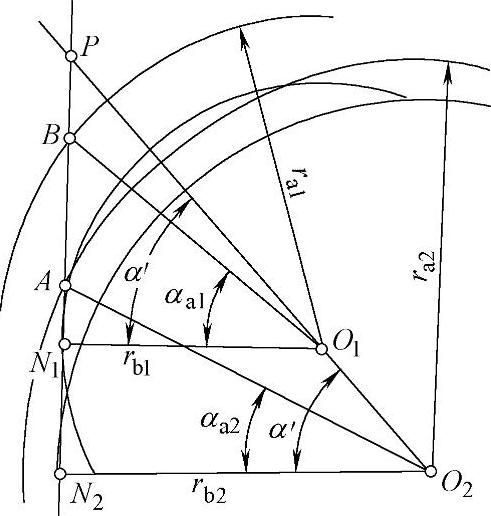
图10-2 无过渡曲线干涉的少齿差内齿轮副的啮合状态

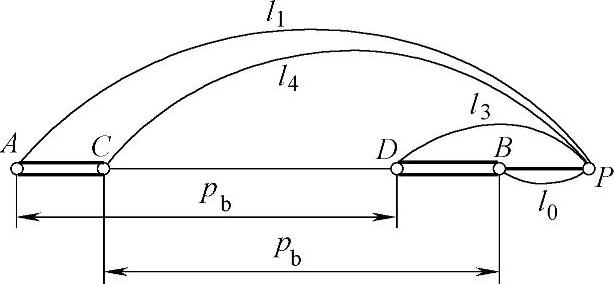
图10-3 1＜ε_α＜2时的接触点轨迹

代入上式得

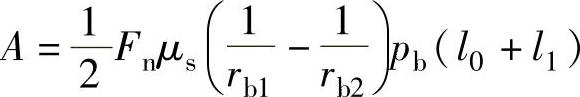
又

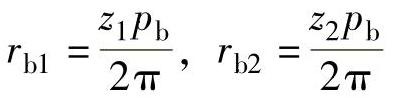
因此

从图10-3可知，一齿的驱动功为

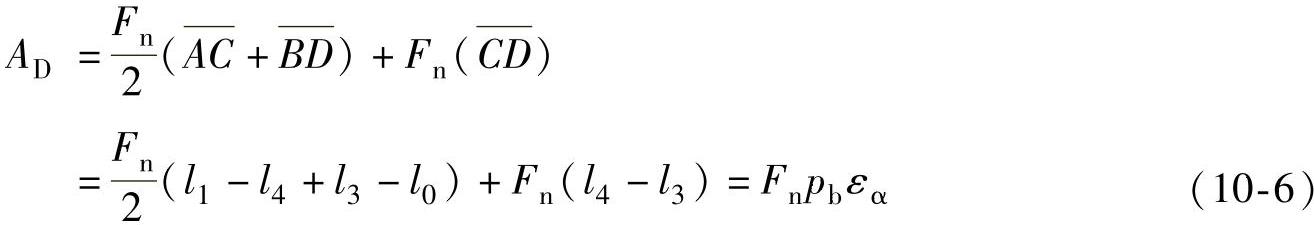
转化机构的啮合效率为

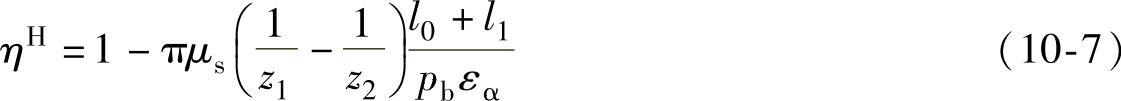(https://www.daowen.com)

式中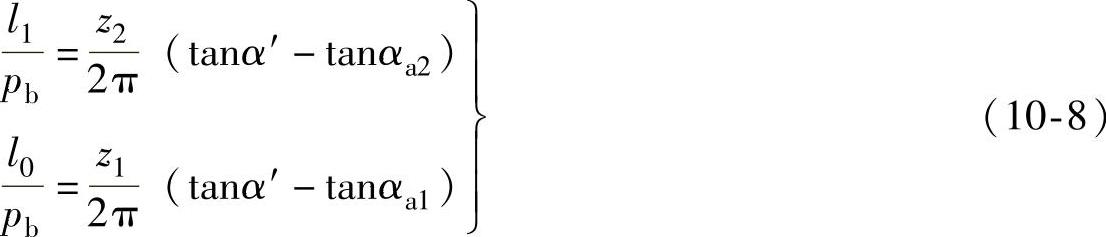

此时的重合度ε_α为

图10-4表示2＜ε_α＜3时的接触点轨迹。根据式（10-4），在一齿啮合期间的摩擦功A为

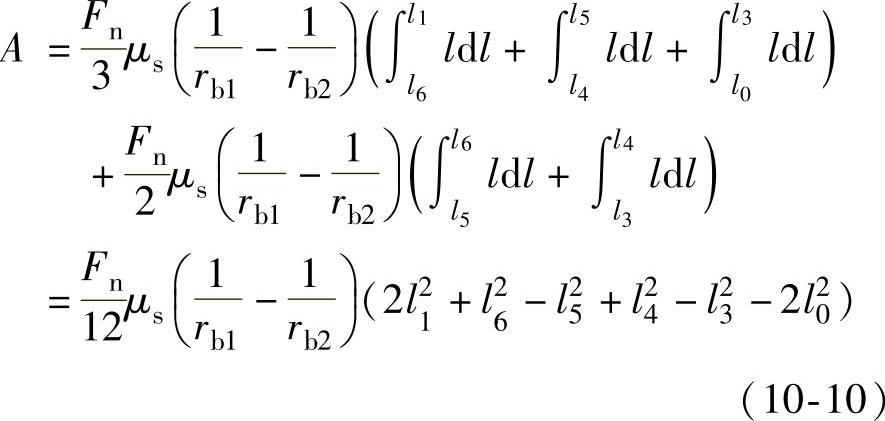
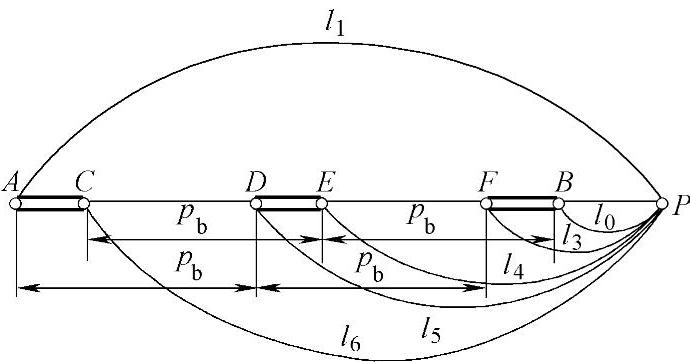
图10-4 2＜ε_α＜3时的接触点轨迹

根据图10-4可知，l₃=l₁-2p_b，l₄=l₀+p_b，l₅=l₁-p_b，l₆=l₀+2p_b。代入式（10-10）得

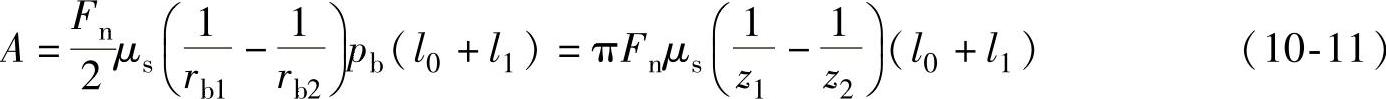
上式与式（10-5）相同。此外，一齿的驱动功A_D=F_np_b。因此，这时转化机构的啮合效率η^H也可用式（10-7）来计算。

现对α=20°，外齿轮不变位，取z₁=40、60、80三种，同与之啮合的内齿轮正变位，齿数比外齿轮多1、2、3，…，8齿，分别计算啮合效率。

在计算中，当齿数差很少，而α′＞α_a1时，齿轮只在节点一侧啮合，效率计算可采用式（10-7）与式（10-8）。齿数差一增加，就变成α′＜α_a1，节点在啮合线之中，实现渐近啮合与渐远啮合。当1＜ε_α＜2时，效率可用下列公式计算：

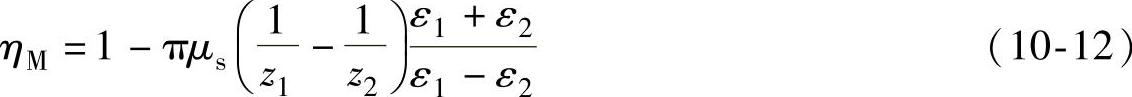
式中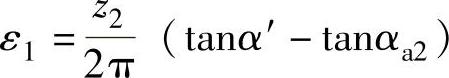，，为渐近啮合；

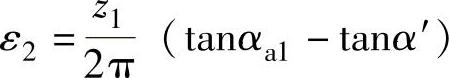，为渐远啮合。

当2＜ε_α＜3时，效率可用如下公式计算：

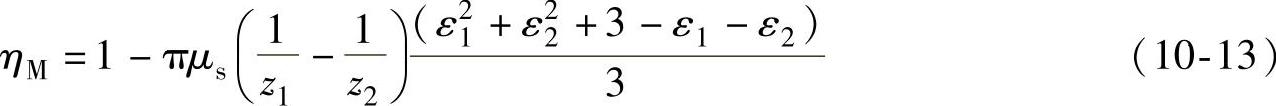
计算结果列于表10-1～表10-3。图10-5为表10-1～表10-3的效率曲线图。

表10-1 渐开线少齿差内齿轮副啮合效率（α=20°，z₁=40）

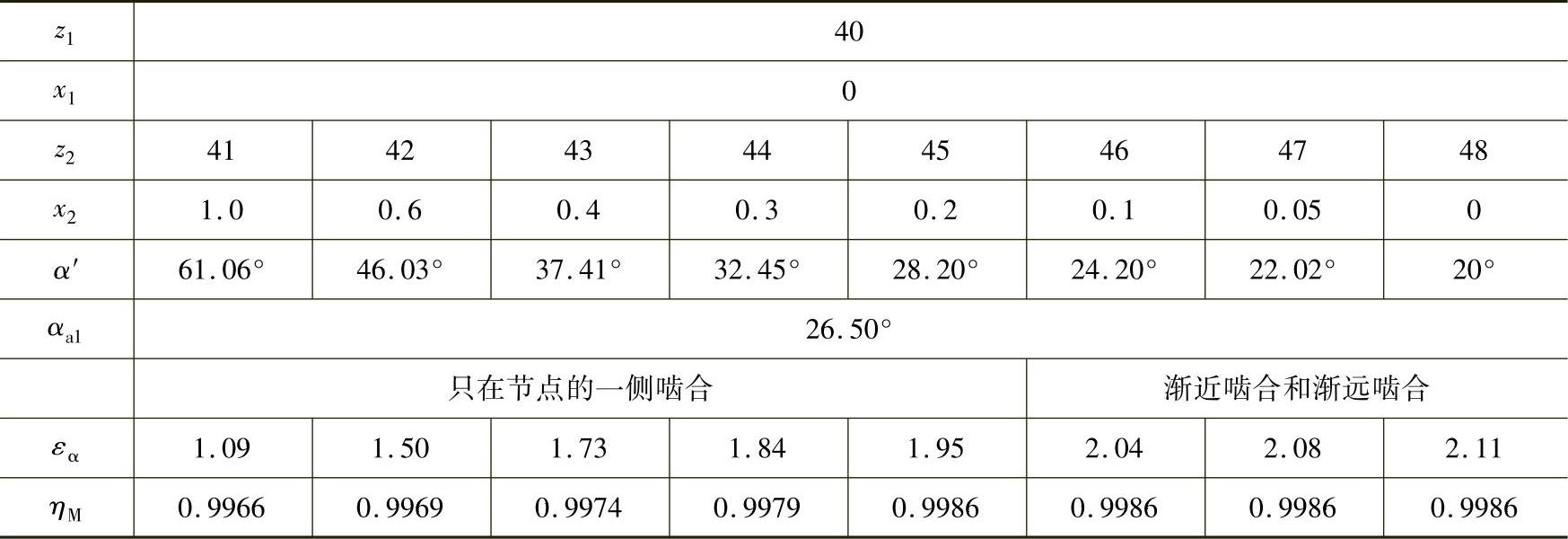
表10-2 渐开线少齿差内齿轮副啮合效率（α=20°，z₁=60）

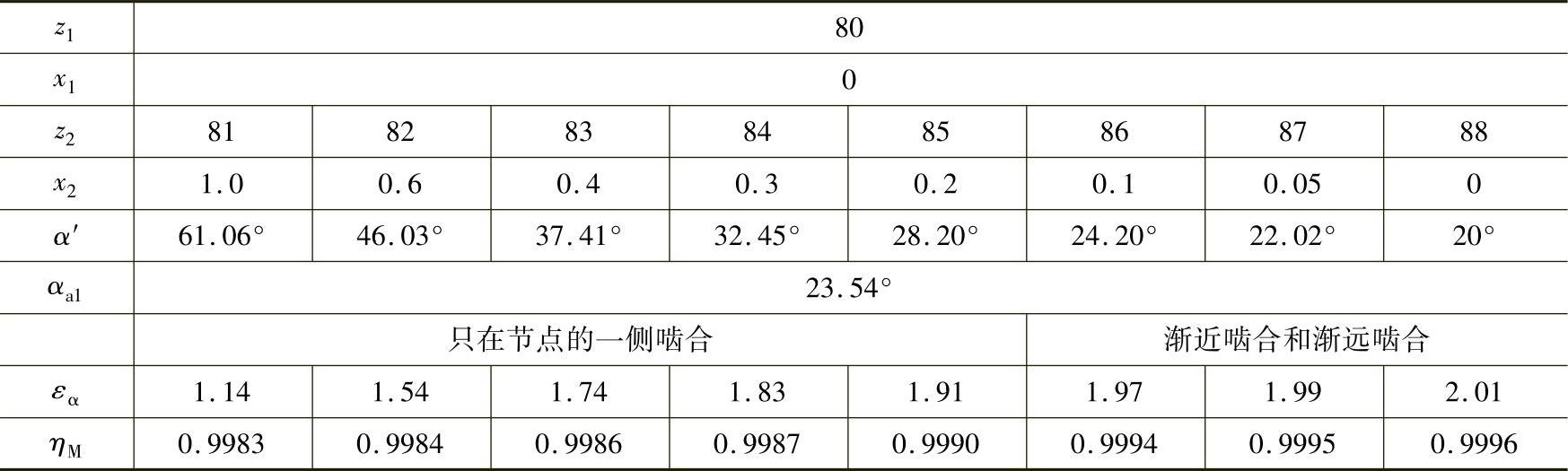
表10-3 渐开线少齿差内齿轮副啮合效率（α=20°，z₁=80）

由图10-5可知，当齿数差很小时（例如z₂-z₁=1），由于啮合角α′较大，滑动摩擦损失较大，所以啮合效率较低。

在齿数差相同的情况下，啮合效率与齿数有关，当齿数z₁较大时，效率稍有提高。

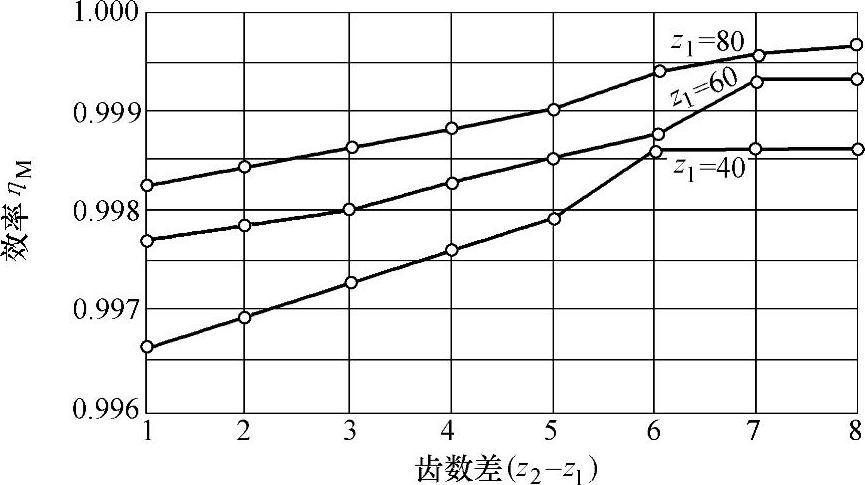
图10-5 效率曲线图