变位系数的选择，应使其既满足啮合方程式，又满足有关的限制条件。主要的限制条件有：

（1）保证重合度ε_α＞1 设计时推荐ε_α=1.1～1.2。重合度的计算式：

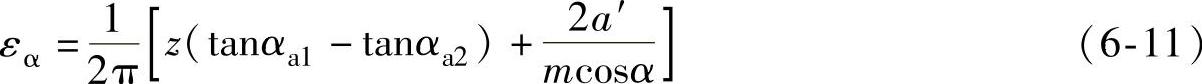
式中，z=z₂=z₁（内、外齿轮的齿数）。

（2）齿顶厚s_a≥（0.25～0.4）m 齿顶厚的计算公式如下：

外齿轮齿顶厚

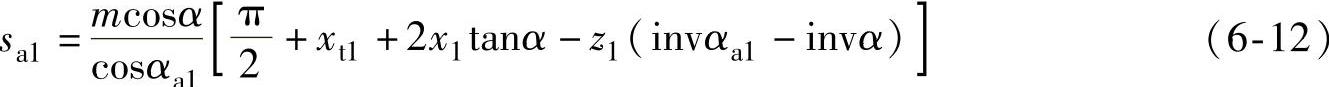
内齿轮齿顶厚

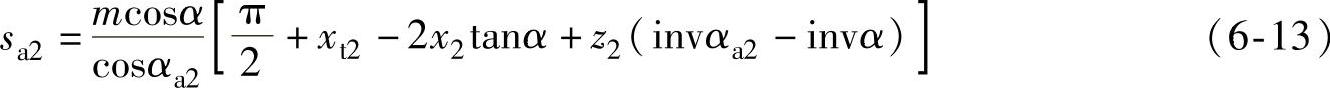
式中 α_a2、α_a1——内、外齿轮的齿顶压力角。

（3）存在合适的齿顶间隙（c^∗＞0） 顶隙系数验算公式如下：

1）外齿轮齿根与内齿轮齿顶之间的齿顶间隙。外齿轮采用滚齿法加工时：

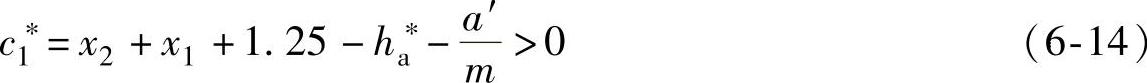
外齿轮采用插齿法加工时：

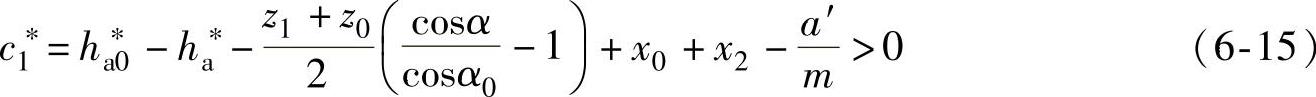
2）内齿轮齿根与外齿轮齿顶之间的齿顶间隙：

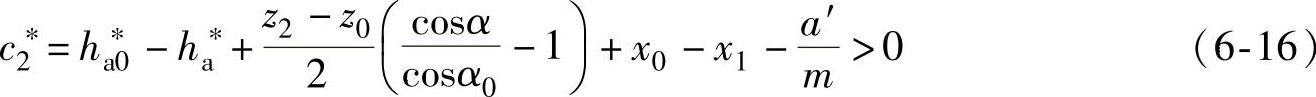
式中 h_a^∗——齿顶高系数，这里推荐h_a^∗=0.8；

h^∗_a0——插齿刀齿顶高系数；

x₀——插齿刀变位系数；

z₀——插齿刀齿数；

α₀——插齿加工时的啮合角。

（4）验算过渡曲线干涉和渐开线干涉 从啮合方程出发，在给定中心距a′和齿形角α之后，待求的参数就是x₁、x₂、x_τ1、x_τ2。

由于零齿差的模数总是选得比少齿差的模数大一些（一般大0.5～1倍），所以零齿差的齿数有时比较少。在这种情况下，应在保证插内齿时不产生径向进刀顶切和齿顶厚度足够的前提下确定x₂。其次，再根据重合度的要求确定外齿轮的变位系数x₁。由式（6-11）可知，切向变位系数与ε_α无关，只要a、α及x₂为不变的常量，便可按重合度的预期值[ε_α]求得相应的x₁。其迭代程序如下：

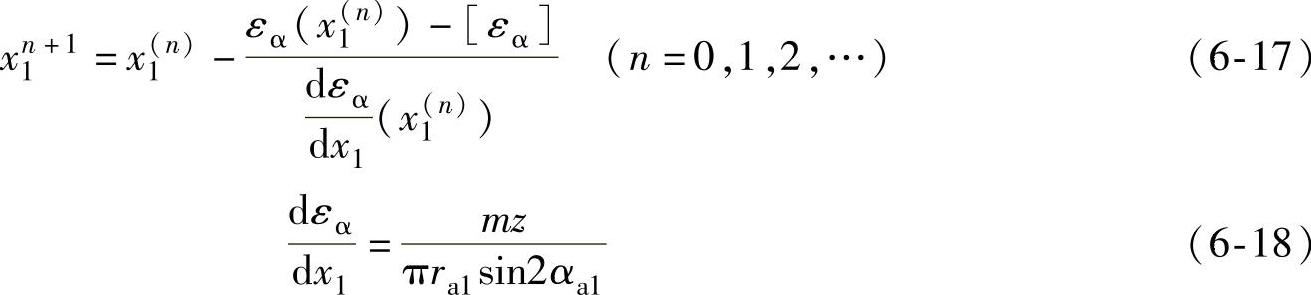
式中 [ε_α]———重合度的预期值；(www.daowen.com)

r_a1———外齿轮的齿顶圆半径。

确定x₁及x₂之后，可由啮合方程求得切向变位系数之和（x_t1+x_t2）。分配x_t1和x_t2的原则是使内、外齿轮的齿顶尽量趋于相等。

x₁、x₂的确定也可用封闭图法。图6-5为零齿差内啮合封闭图，由下列曲线组成。

1——重合度ε_α=1的限制图线；

2——外齿轮z₁齿顶厚s_a1=0的限制曲线；

3——内齿轮z₂齿顶厚s_a2=0的限制曲线；

4——内齿轮z₂纵向齿廓与外齿轮z₁齿根过渡曲面干涉的限制曲线；

5——齿轮z₁纵向齿廓与内齿轮z₂齿根过渡曲面干涉的限制曲线；

6——外齿轮z₁与插齿刀齿根过渡曲面产生顶切干涉的限制曲线；

7——齿高h=2.5m的限制曲线；

8——啮合角α′=0的限制曲线；

9——重合度ε_α=1.2的限制曲线；

10——齿顶厚s_a1=0.25m的限制曲线。

此外，z₁=z₂=36，z₀=18的封闭图如图6-6所示；z₁=z₂=44，z₀=15的封闭图如图6-7所示；z₁=z₂=44，z₀=22的封闭图如图6-8所示；z₁=z₂=50，z₀=15的封闭图如图6-9所示。

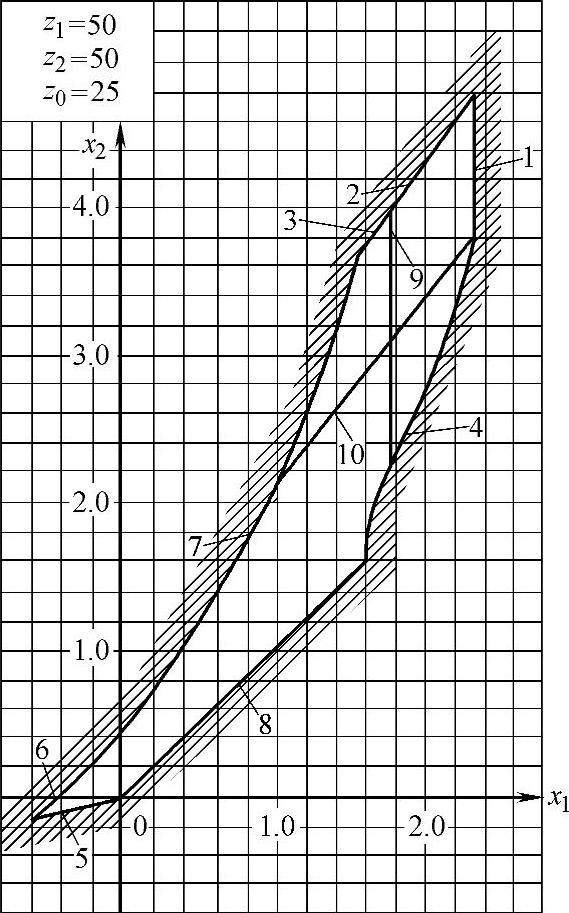
图6-5 零齿差内啮合齿轮传动封闭图

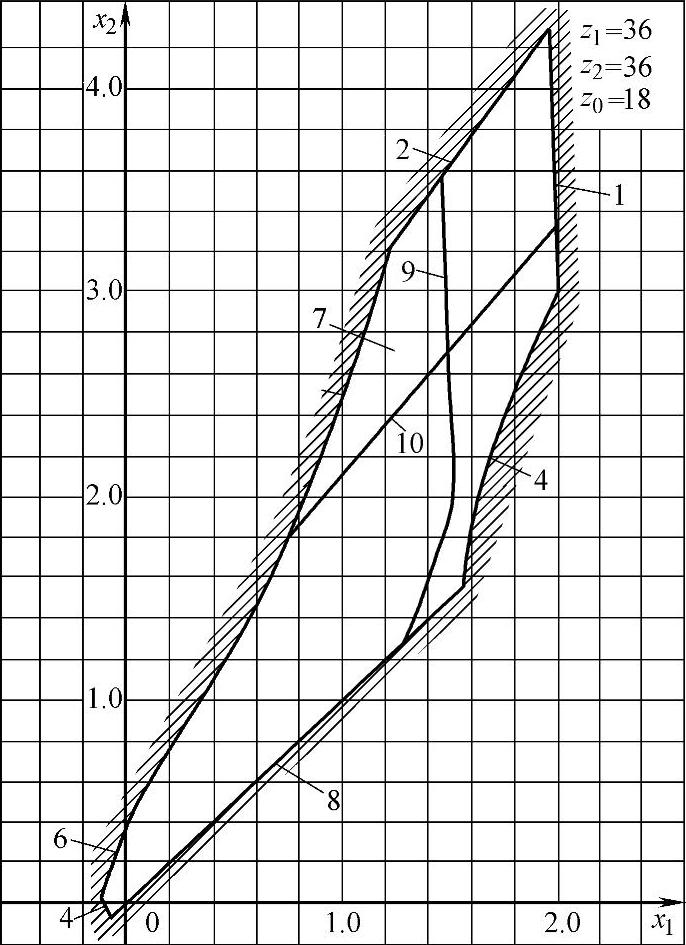
图6-6 z₁=z₂=36，z₀=18的封闭图

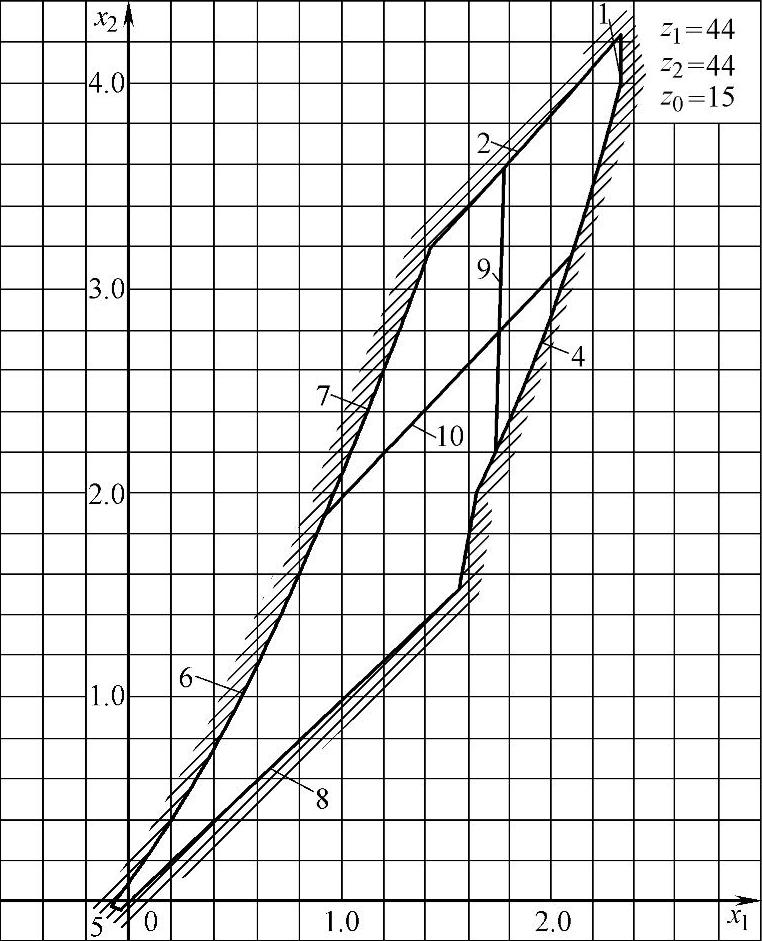
图6-7 z₁=z₂=44，z₀=15的封闭图

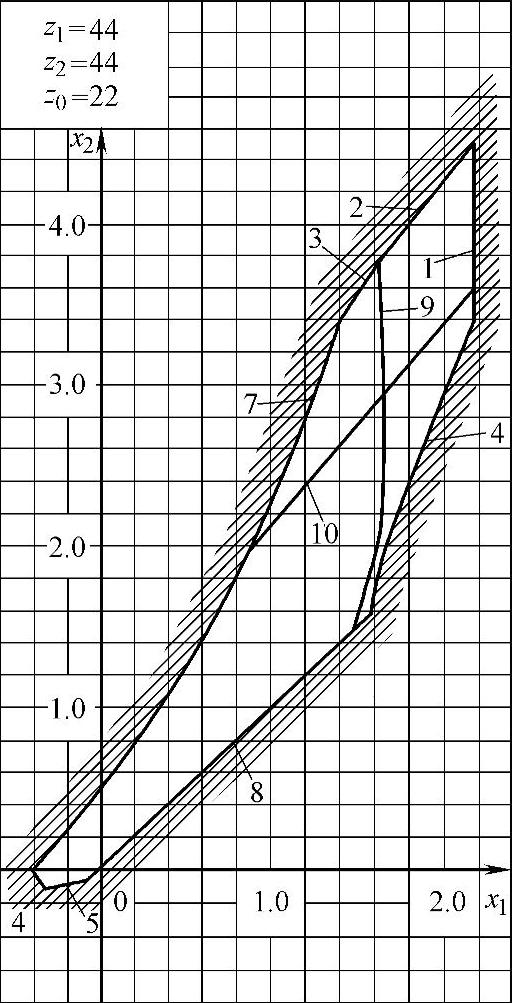
图6-8 z₁=z₂=44，z₀=22的封闭图

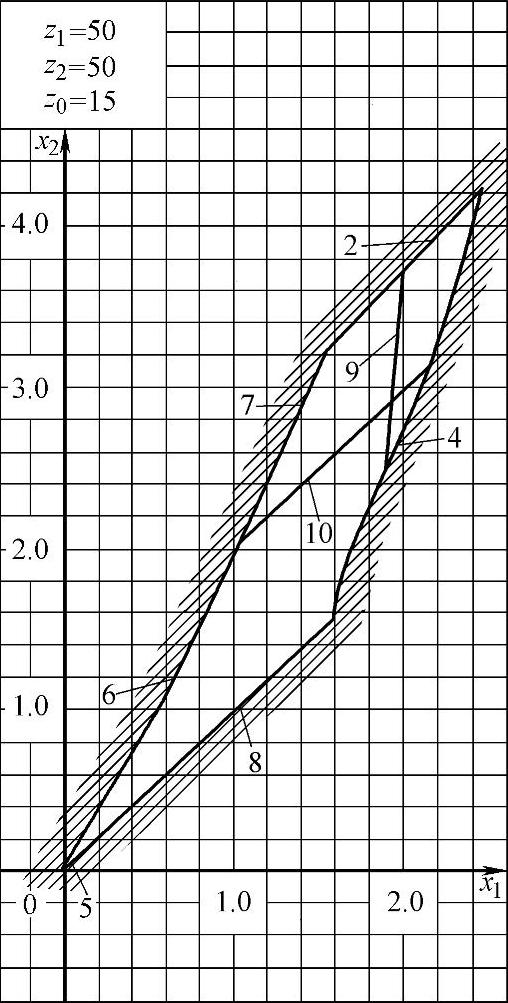
图6-9 z₁=z₂=50，z₀=15的封闭图