由公式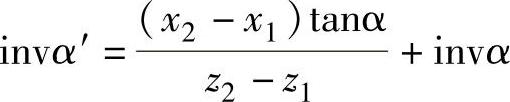可知，当z₂-z₁=0，α′=90°时，一般的几何计算公式不适用，因为z_∑=z₂-z₁=0、α′=90°，上面公式变成不确定的，但可利用图6-1，得到不定式的展开计算式。

如果齿轮z₁、z₂的中心线与齿轮2的齿槽、齿轮1的轮齿对称线重合时，则其齿廓位于等距线之间，并形成侧隙，其沿齿廓法线方向的大小，等于沿基圆方向齿轮2的齿槽宽与齿轮1的齿厚之差的一半，可由下式确定：

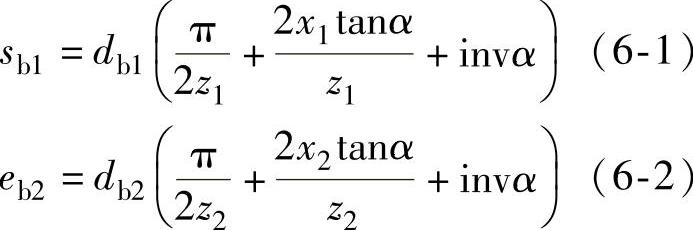
为了得到无侧隙啮合，需将一齿轮相对另一齿轮平移一侧隙大小，其中心距为

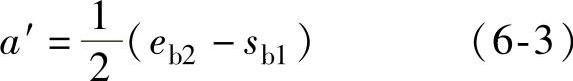
因为在这种情况下，d_b1=d_b2、z₁=z₂，经变换后得

a′=m（x₂-x₁）sinα （6-4）

如果涉及大、小齿轮的切向变位（小齿轮的切向变位系数为x_τ1、内齿轮为x_τ2）形成侧隙在内，则中心距a′应为

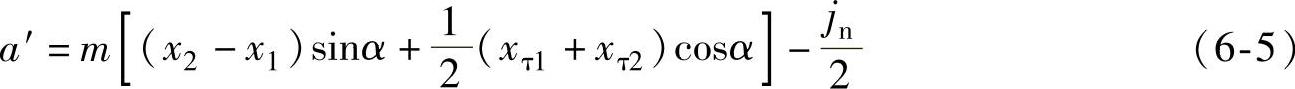
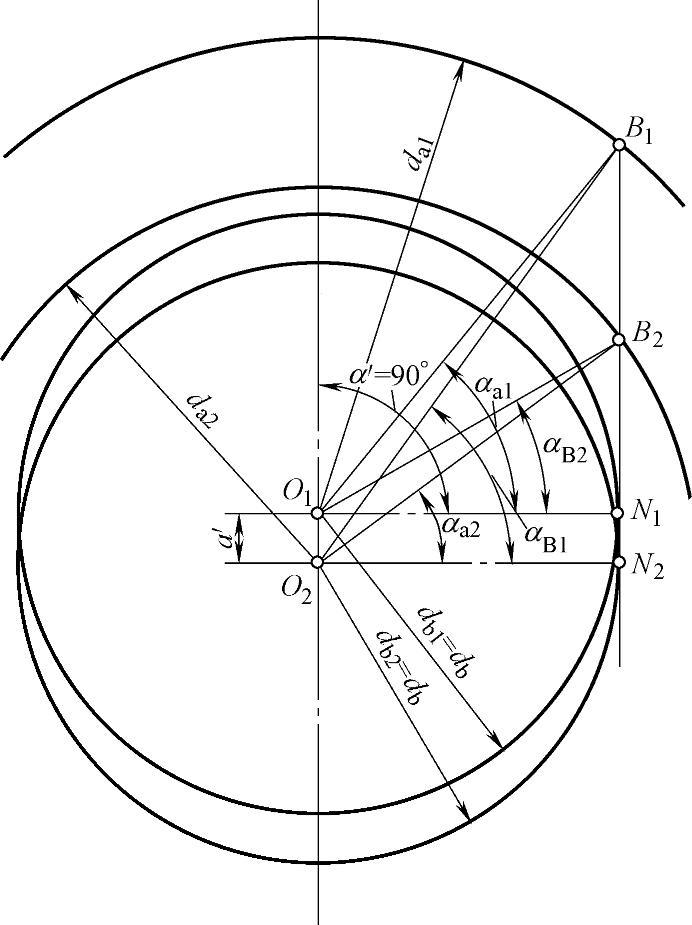
图6-1 当z₁=z₂、α′=90°时，内啮合齿轮副参数的确定

式中 j_n——啮合侧隙（见图6-2），设计时可按j_n=0进行。

根据图6-1也可确定重合度。当不考虑齿轮的切向变位时，则

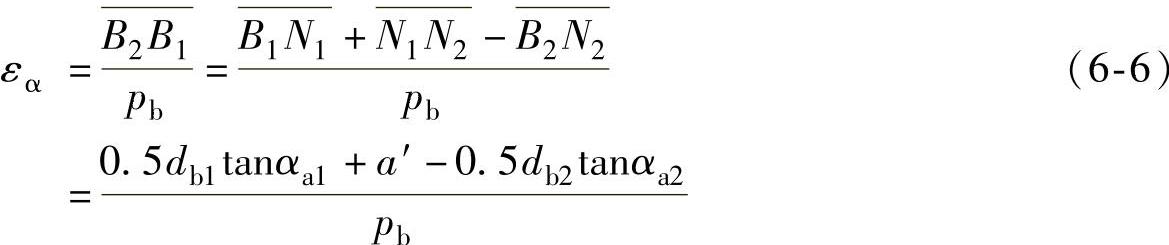
经变换后，得

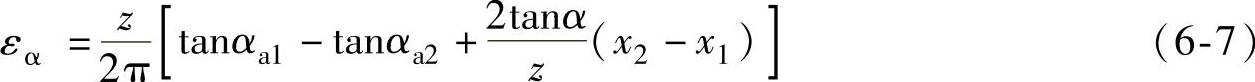
齿廓工作部分起始点的压力角由下式确定：

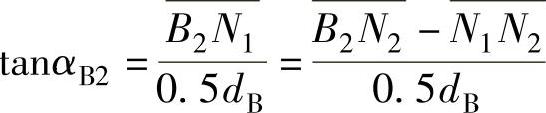(www.daowen.com)

变换后，得

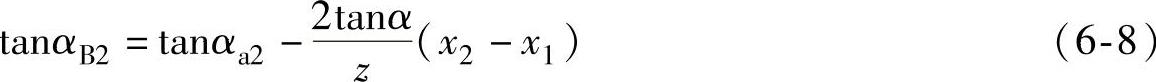
同理得

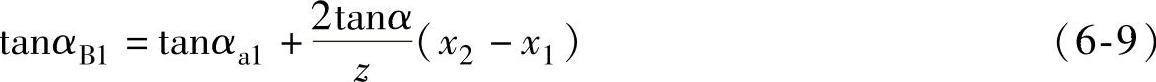
其他几何计算和一般内啮合传动的计算没有什么区别，通常是按几何指标校核啮合质量，只有齿廓重叠干涉无需校核。这种形式的干涉，在本传动中原则上不可能产生的，因为齿轮1的每一轮齿始终保持在齿轮2的同一齿槽中。

z_∑=0的传动具有特殊的特性，在啮合线上的滑动速度是不变的，则

v_s=a′w （6-10）

变位系数的选择根据封闭图确定。图6-3所示为典型封闭图之一，是根据顶隙保持不变

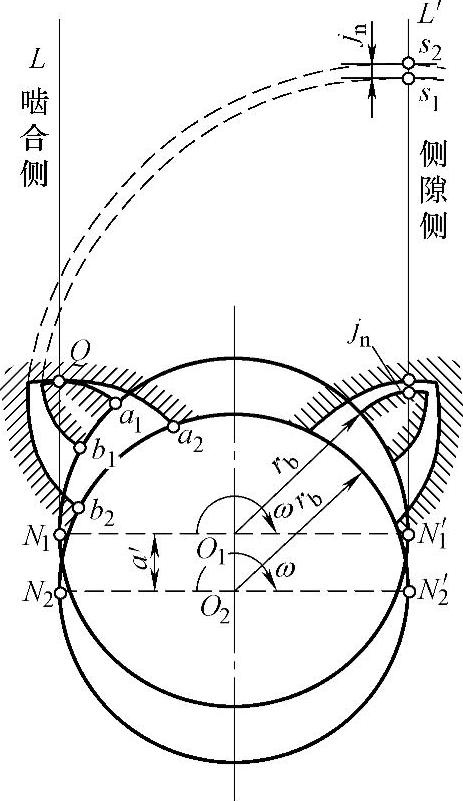
图6-2 零齿差变位渐开线内齿轮啮合

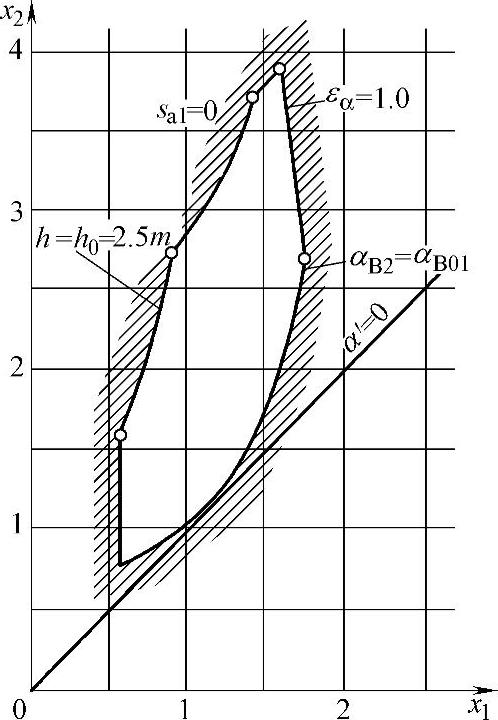
图6-3 当z₁=z₂=30，α′=90°、z₀=15、x₀=0.104时，内啮合齿轮副的封闭图

的计算系统拟制的。其中外齿轮1用滚刀加工，内齿轮用z₀=15、x₀=0.104标准插齿刀加工。从中可以看出，传动的可能性组合，变位系数具有很大的变化范围。

图6-4所示为零齿差z_∑=0的传动简图。当齿轮中心线固定时，这种传动可用作联轴器，连接两平行且不同心的轴。在行星传动中，行星轮作平动，并且其任意点的轨迹是直径为2a′的圆。

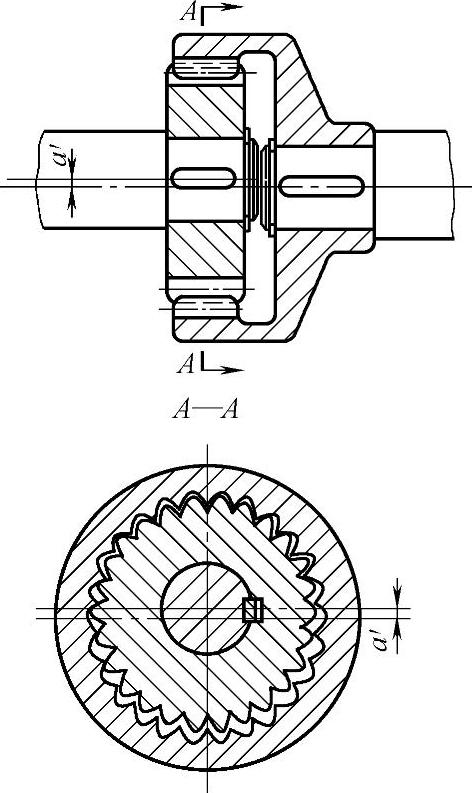
图6-4 零齿差内齿轮副