随着计算机的普及，借助计算机的辅助设计与分析，将变位系数的选取和齿轮其他参数一起用计算机完成，列成表格，直接查表选用，十分方便。计算原则是在选取变位系数时，既要满足G_s＞0，但也不宜过大，预先给定一个很小的值，G_s=0.05，然后解出变位系数与齿轮其他参数。显然这样做使重合度提高，变位系数减小，较为合理。

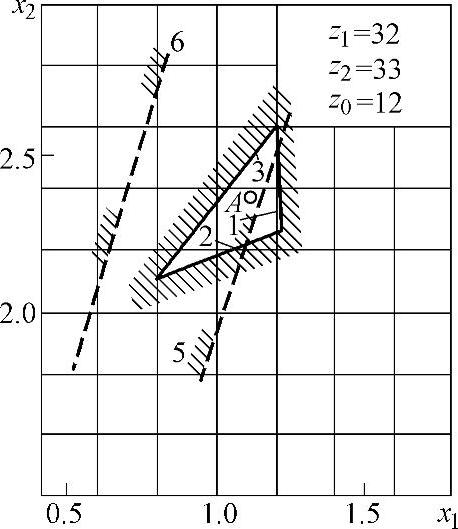
图5-10

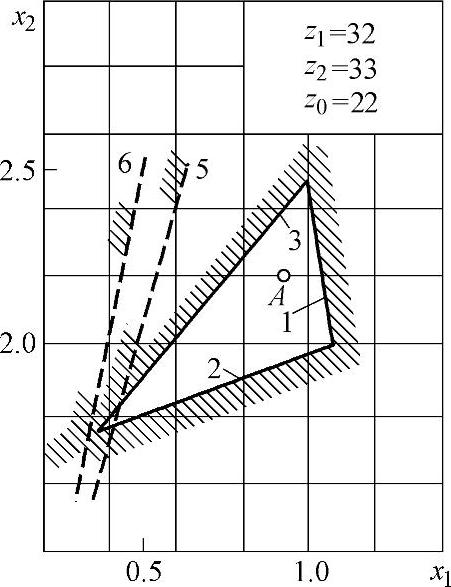
图5-11

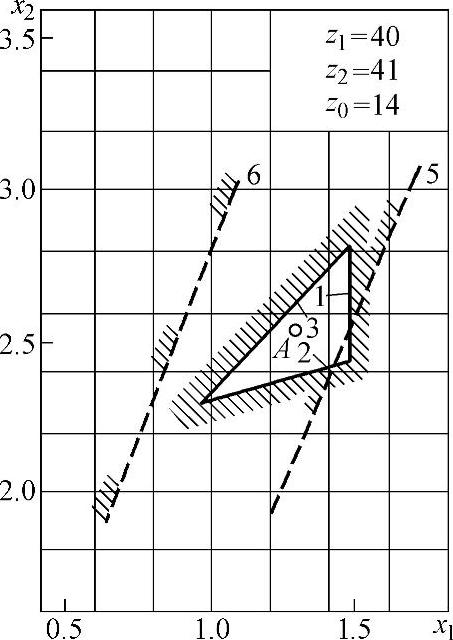
图5-12

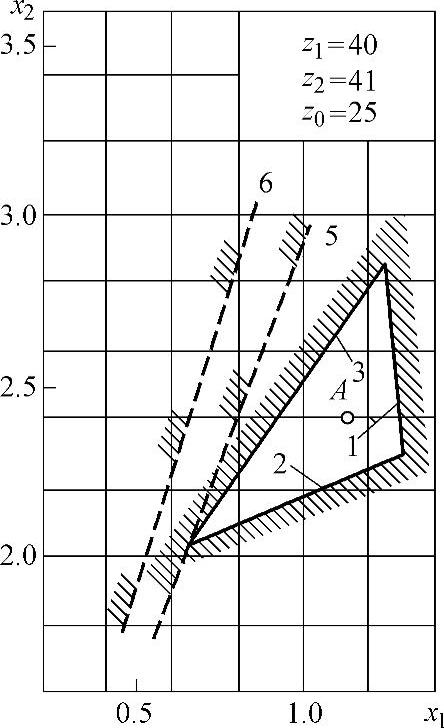
图5-13

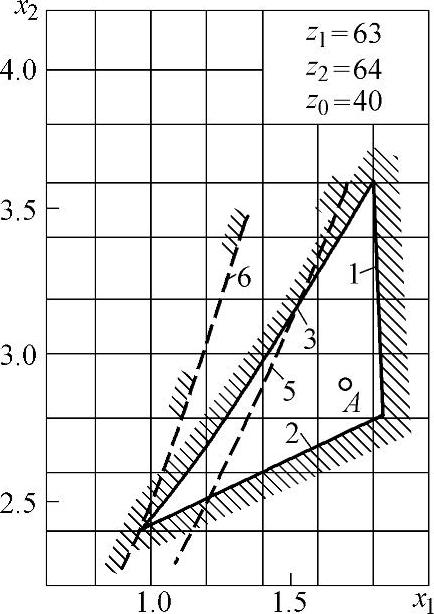
图5-14

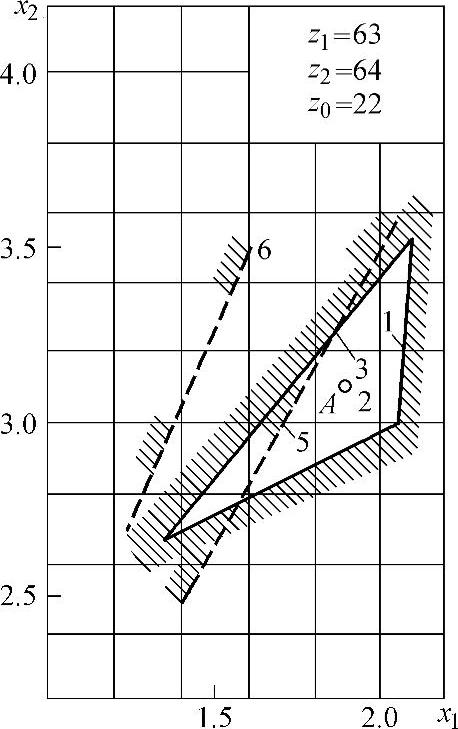
图5-15

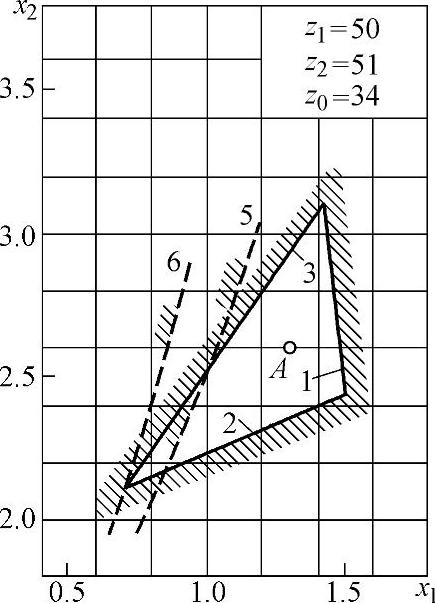
图5-16

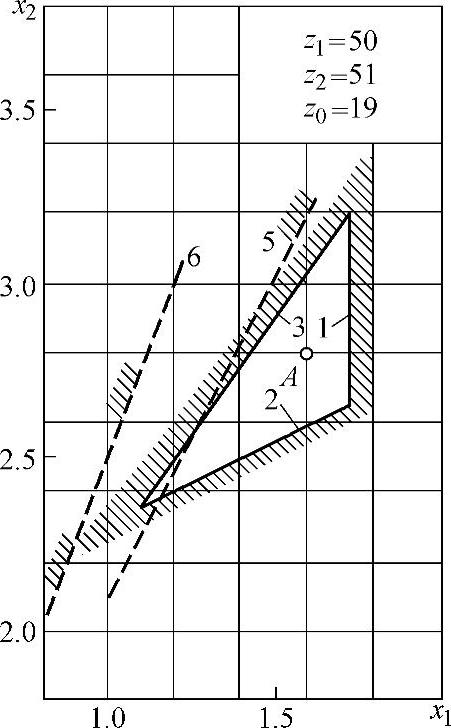
图5-17

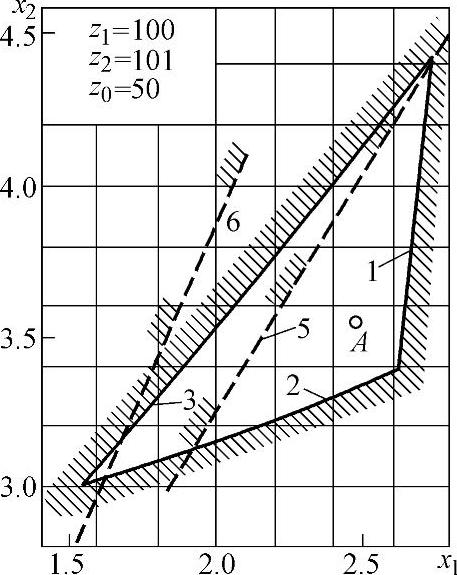
图5-18

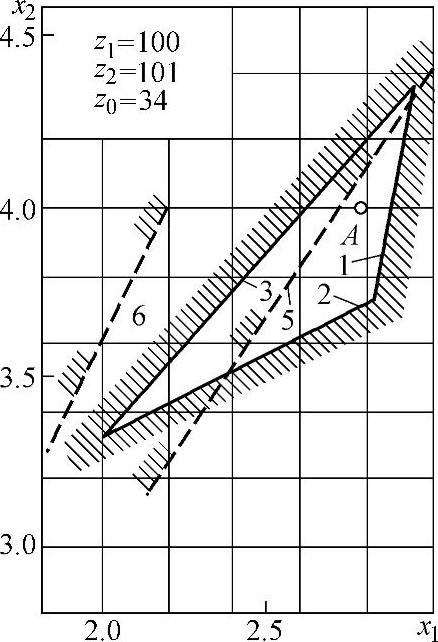
图5-19

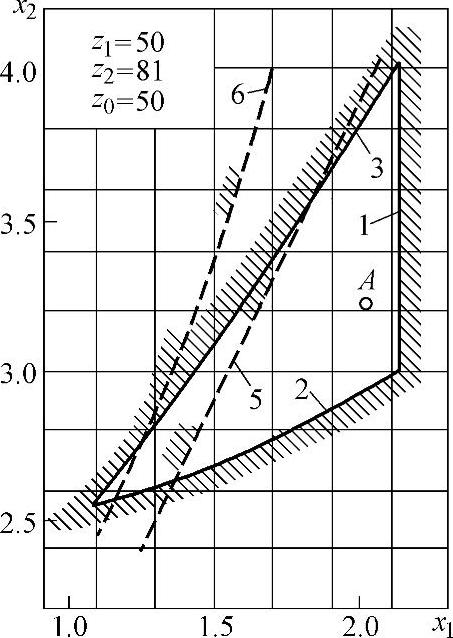
图5-20

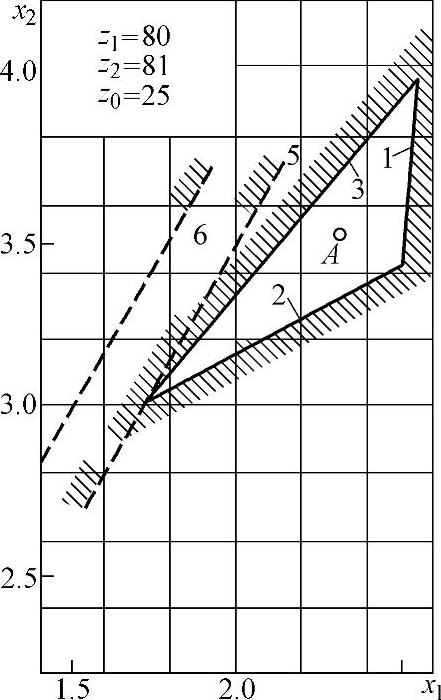
图5-21

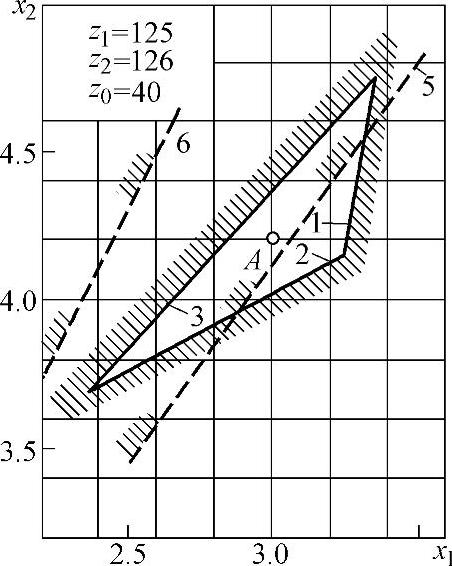
图5-22

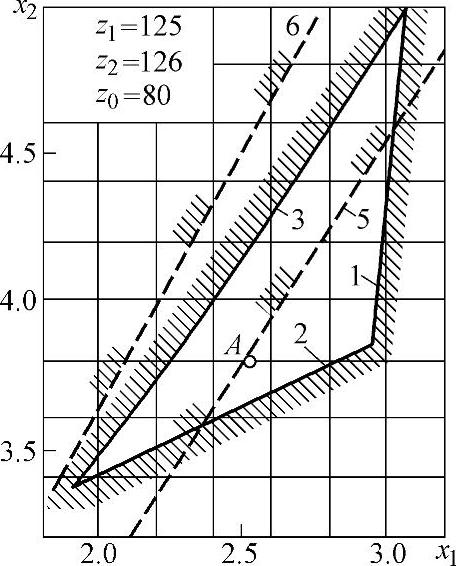
图5-23

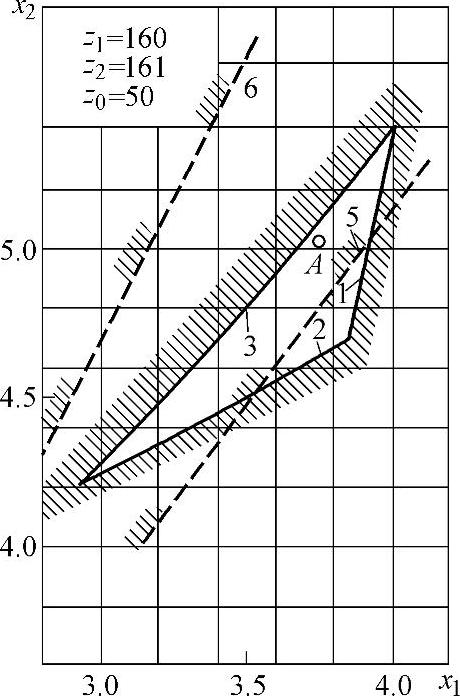
图5-24

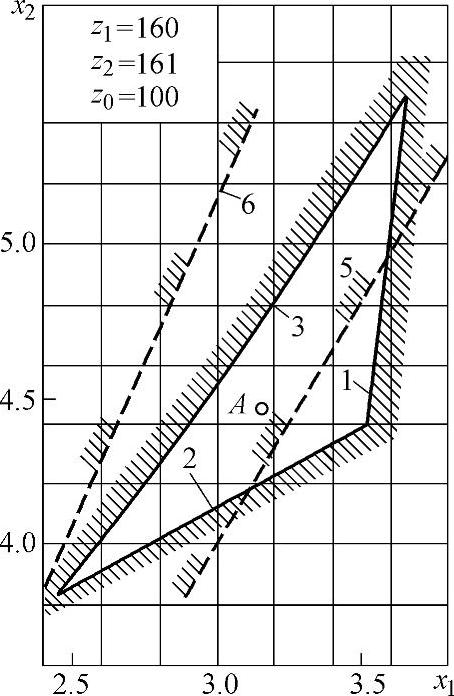
图5-25

目前较流行的是按啮合角最小的要求，确定少齿差内啮合的变位系数；以及啮合角已知时，变位系数的确定。现将这两种方法作一论述。

（1）按啮合角最小的要求确定少齿差内啮合齿轮副的变位系数

根据分析，齿数差很少的内啮合，其啮合角的最小值，由限制条件ε_α、G_s、s_a1所决定。为减小啮合角，应取三条曲线中某两条曲线的交点作为变位系数。

首先分析ε_α与G_s两条曲线的交点。根据前面的论述，ε_α和G_s应满足的条件如下：

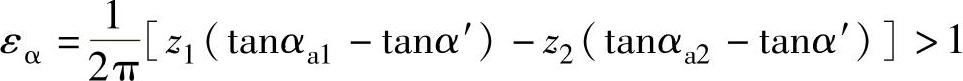
设计时，ε_α可以取大于1的所需值，在此我们取ε_α=1求解作为示例，即

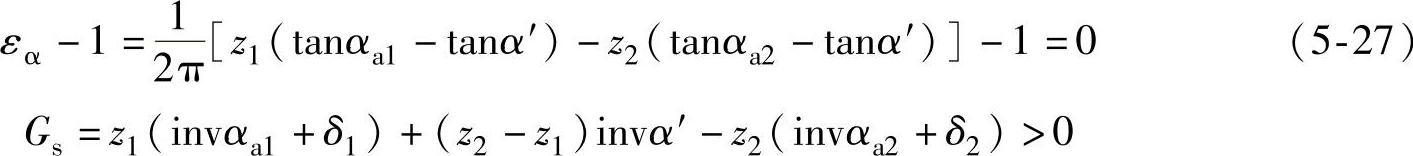
设计时，G_s可取大于零的所需值，作为示例，在此取G_s=0求解，即

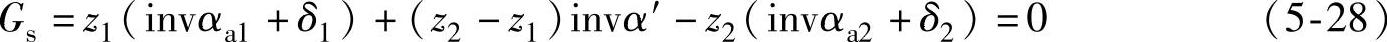
把变位系数x₁、x₂作为独立变量，把α′作为中间变量，因α′可由啮合方程作为x₁、x₂的已知函数。用牛顿法求解，其迭代程序为

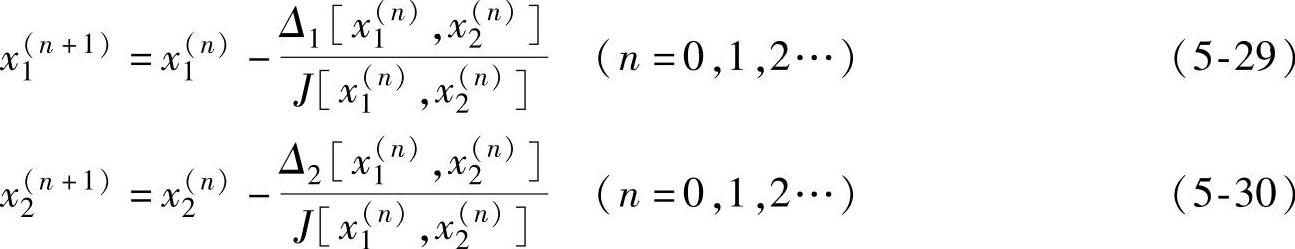
式中

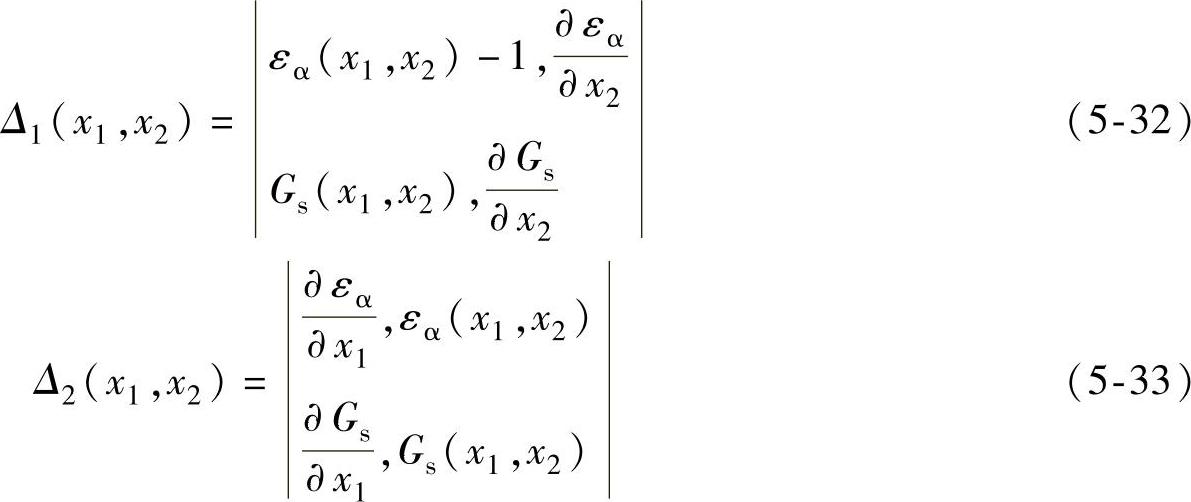
计算时，只要初始值（x₁^（0），x₂^（0））选得充分接近方程组（5-27）、（5-28）的精确解（x₁，x₂），牛顿方程（5-29）和方程（5-30）就会收敛。

当齿顶圆半径用

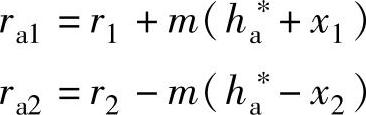
计算时，行列式元素是：

由式（5-29）及（5-30）所求得的x₁及x₂，即为图5-26中的交点T。此点是否满足s_a1的需求，尚须验算，验算式如下：(www.daowen.com)

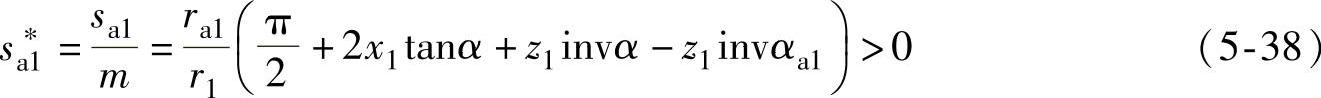
设计时，s^∗_a1可取大于零的所需数值。

若T点不能满足式（5-38）的要求，则α_min在G_s与s^∗_a1的交点（见图5-27），求解此交点的方法与上述相同，但需要用到下列行列式元素，即

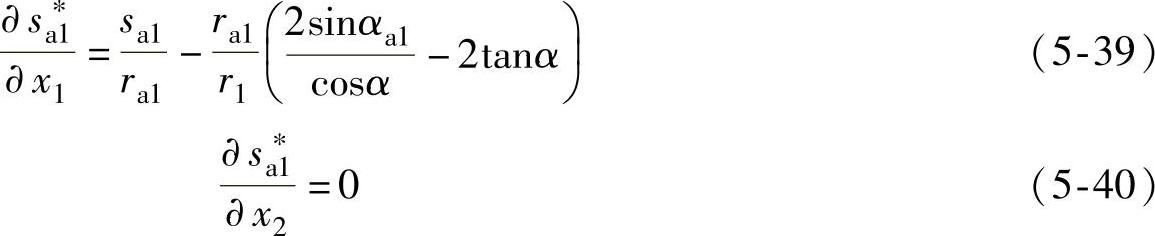
需要指出的是，上述各行列式元素是当齿顶圆半径用r_a1=r₁+m（h_a^∗+x₁）及r_a2=r₂-m（h_a^∗-x₂）计算时推导的。若齿顶圆半径用其他公式计算，则行列式元素也要另行推导。

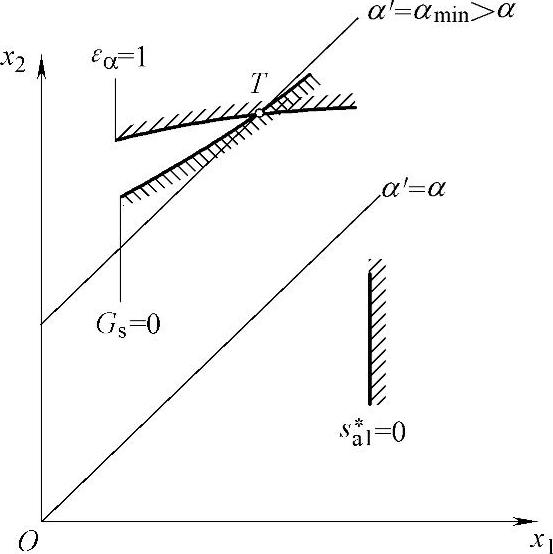
图5-26 图示限制条件下的变位系数

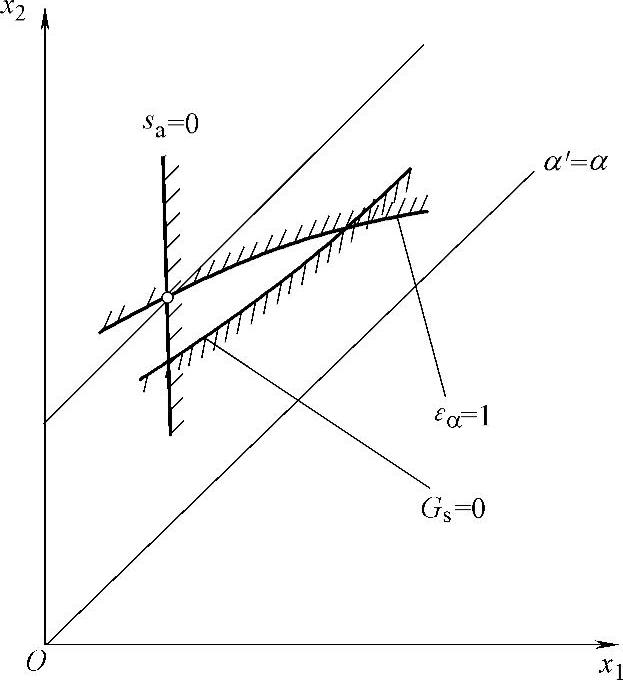
图5-27 图示限制条件下的变位系数

【例5-1】 内啮合齿轮副，z₁=56，z₂=60，h_a^∗=0.8，α=20°，试求ε_α=1及G_s=0时的变位系数x₁及x₂。

解 取x₁^（0）=1及α′=40°。

由啮合方程得x₂^（0）=1.3463566，此时ε_α=1.139236，G_s=0.1464。

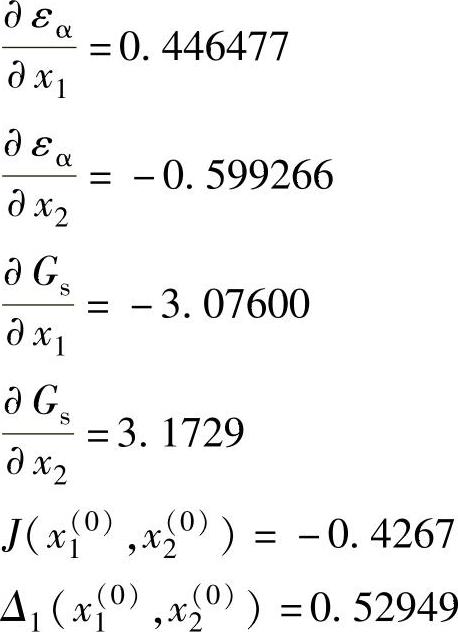
Δ₂（x₁^（0），x₂^（0））=0.49364

代入式（5-29）及式（5-30），求得

x₁^（1）=2.2409

x₂^（1）=2.5033

α′=37.26°

ε_α=1.037

G_s=-0.021

按此方法迭代，最后得到的结果是：

x₁=2.676

x₂=2.935

α′=37.131°

ε_α=1.00

G_s=0.00

（2）啮合角已知时变位系数的确定

在少齿差内啮合齿轮副的设计中，只要选取适当的啮合角，就能同时达到ε_α＞1及G_s＞0的要求。如图5-28所示，当α′不变时，由啮合方程可作出倾斜45°的直线，在A—B之间选取变位系数时，便同时能满足上述两项限制条件的要求（对于一个设计，在需要时，可另行验算s^∗_a1）。

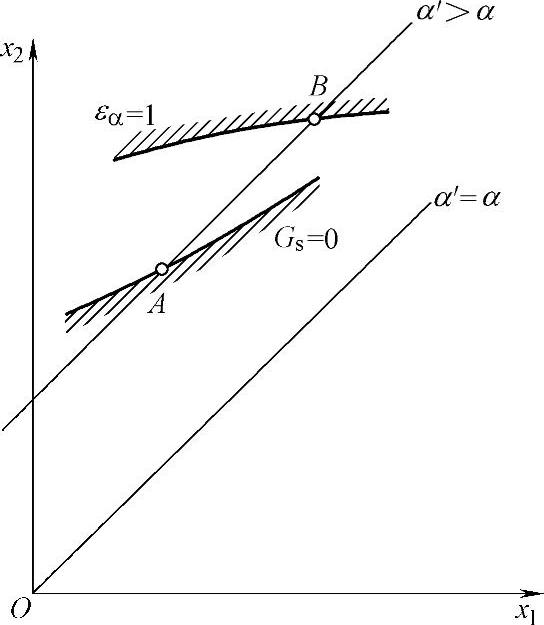
图5-28 图示限制条件下的变位系数

由于α′=常数，使问题得到简化，可以用牛顿法求得ε_α或G_s达到某一预期值时的变位系数。当欲使G_s达到某一预期值，迭代程序如下：

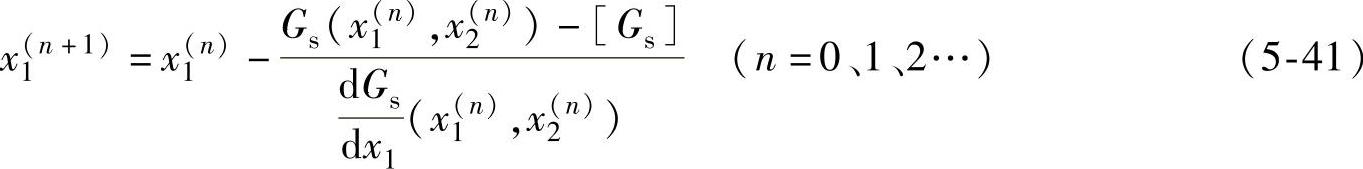
式中，[G_s]为G_s的预期值，在设计时，取[G_s]=0.05左右。

当齿顶圆半径用

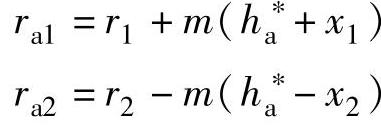
计算时，由推导得

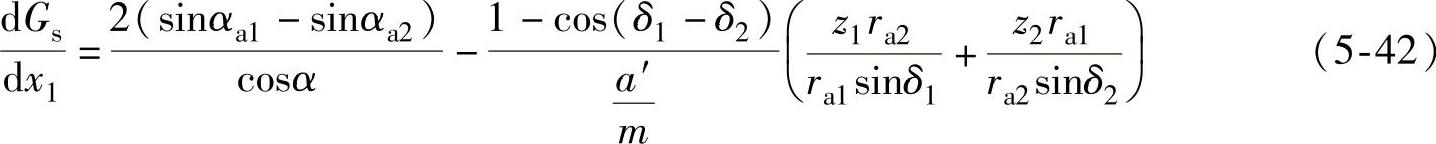
上式第二项可以简化。由于r_a1sinδ₁=r_a2sinδ₂，并取z₁r_a2≈z₂r_a1，在推导过程中，再取mz₂≈2r_a2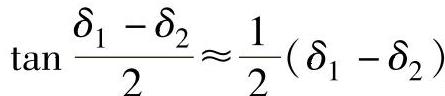，，则式（5-42）可简化为

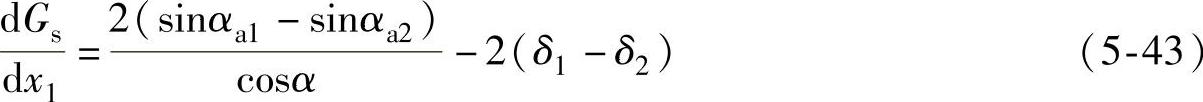
简化以后的导数式十分简单，而不增加迭代次数。

若是按重合度的预期值[ε_α]确定变位系数，只需将式（5-41）中的G_s易为ε_α及[G_s]易为重合度的预期值[ε_α]即可。详见例5-2。导数计算式为

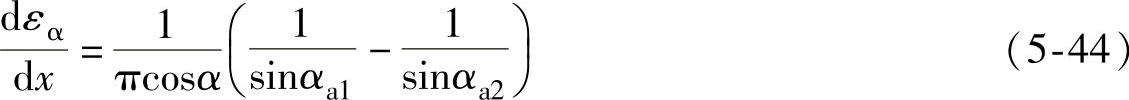
【例5-2】　内啮合齿轮副，m=3mm，α=20°，z₁=51，z₂=52，h_a^∗=0.6，[ε_α]=1.05，试求当α′=49°时x₁、x₂的值。

解　取x₁的初始值，x₁^（0）=0，则

以下按上述顺序继续计算得到

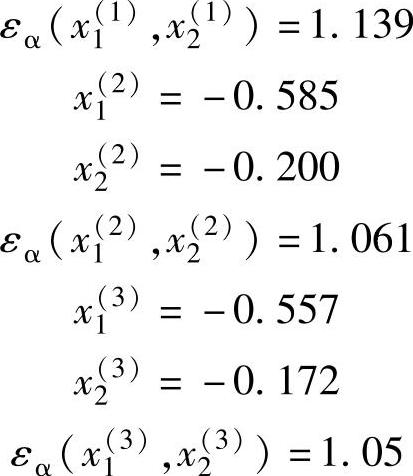
计算至此已满足预期要求，迭代终止。验算齿廓重叠干涉，得到G_s=0.08，满足要求。

关于初始值x₁^（0）的选取颇为重要。初始值越接近精确解，越不易出现其他问题。但在计算开始时，并不知道精确解。因此，建议先取x₁^（0）=0试算。如果计算中出现r_b1≥r_a1时则增大x₁^（0）重新计算，用计算机计算时步长可取0.1，手算时步长可稍大些；若在齿廓重叠干涉验算中，出现cosδ₁或cosδ₂大于1，应立即改取x₁^（0），重新计算。

当h_a^∗取得越小时，满足ε_α或G_s要求的x₁也越小，但此时ε_α或G_s却增大了。这就意味着，同一对齿轮，若取较小的h_a^∗，可使啮合角减小。由于x₁为负值时，还需要考虑避免根切，所以通常在设计时，取h_a^∗的最小值为0.6。