渐开线齿轮传动的重要特性之一是齿面间存在相对滑动。而且这种滑动无法避免。设计者应当了解相对滑动的原理和计算，以便在设计时予以减轻。行之有效的方法便是调整啮合的起始点及啮合终止点的位置。

通常用滑动率来表示齿面间的相对滑动。设内啮合中的外齿轮与内齿轮在任一点K接触（见图4-15），外齿轮主动，内齿轮从动。v_K1、v_K2分别为外齿轮、内齿轮在K点的圆周速度，v_K1t、v_K2t分别为其在K点沿齿面的切向速度。则滑动率η由以下两式表示。

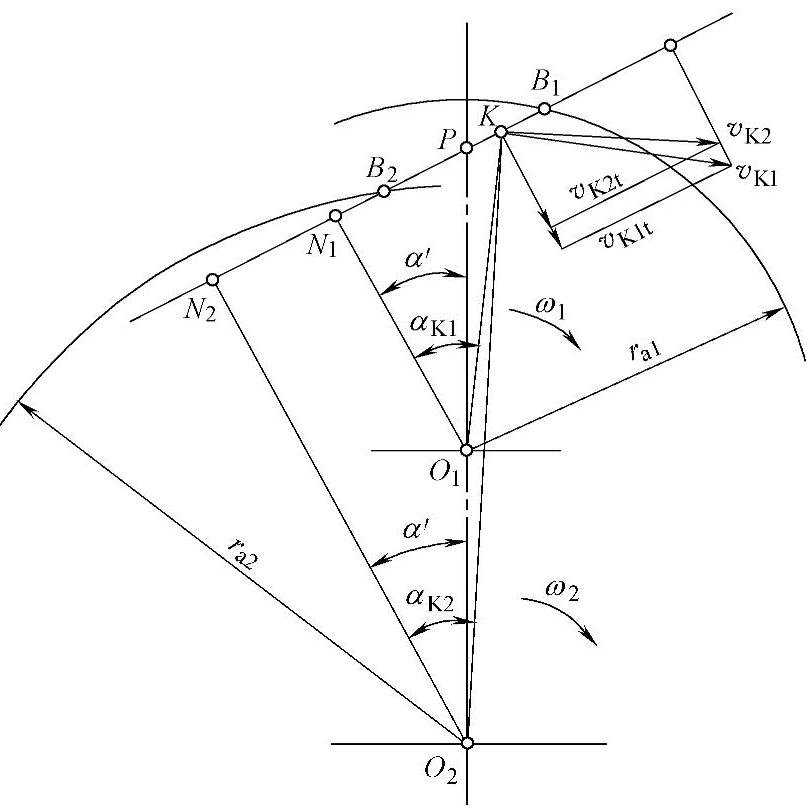
图4-15 滑动率的计算

外齿轮

内齿轮

式中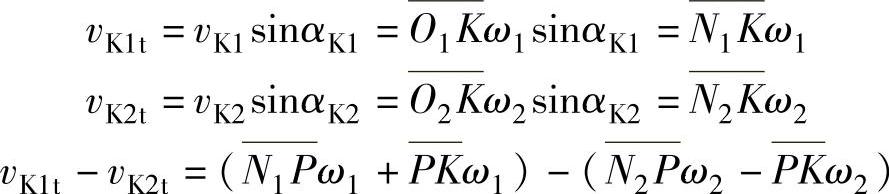

因为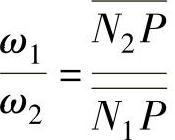

所以 。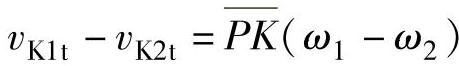

将上述各式代入式（4-50）、式（4-51）得

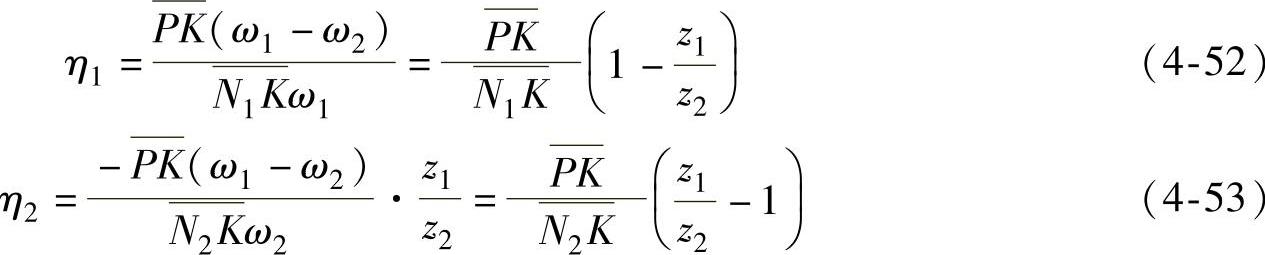
由此可知，滑动率随着啮合点的位置而变化，图4-16为其变化曲线。

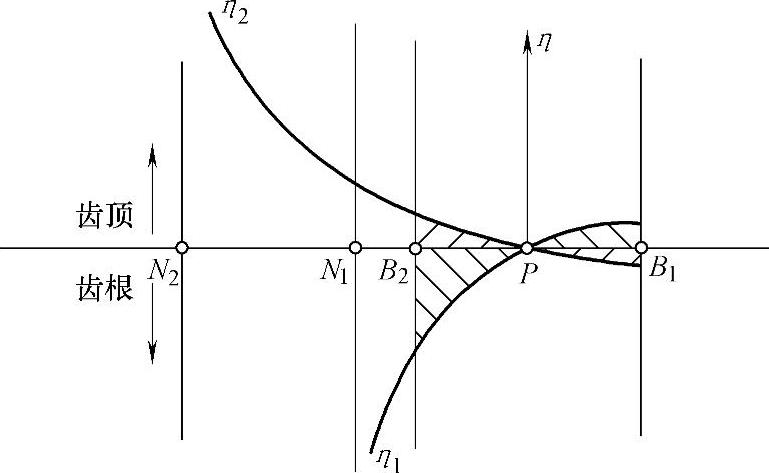
在节点P的滑动率为零。在B₂、B₁点的滑动率，可将有关参数代入式（4-52）及式（4-53）经整理后，由下列各式表示。

外齿轮齿根部的滑动率

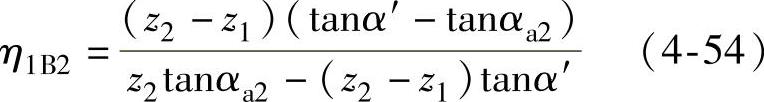
外齿轮齿顶部的滑动率

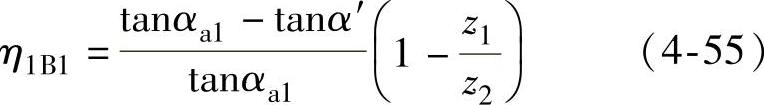
(www.daowen.com)

图4-16 内啮合滑动率变化曲线

内齿轮齿顶部的滑动率

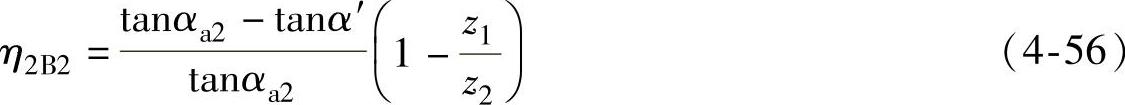
内齿轮齿根部的滑动率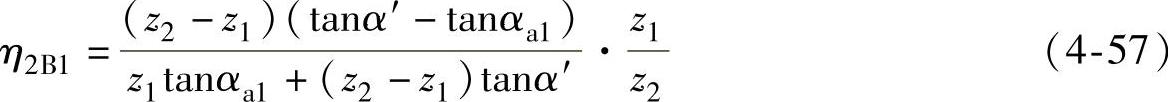

由于相对滑动速度方向不同，由上述各式求得的滑动率有正负之分。但是判断相对滑动的大小，是以滑动率的绝对值为依据的，即滑动率的绝对值不应超过许用值。而通常所说的滑动率也都是指其绝对值而言。滑动率是一个比值，所以其许用值与齿轮的节圆的圆周速度有关，如表4-8所示。

表4-8 滑动率的许用值

【例4-5】 一内啮合标准齿轮副，m=2mm，α=20°，h_a^∗=1，z₁=30，z₂=60，试计算其重合度和滑动率。

解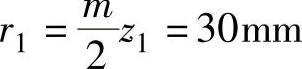

重合度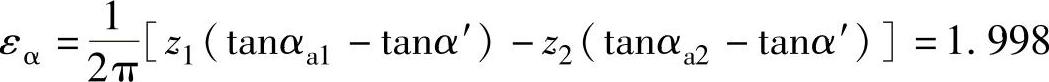

其中α′=α=20°。

滑动率为

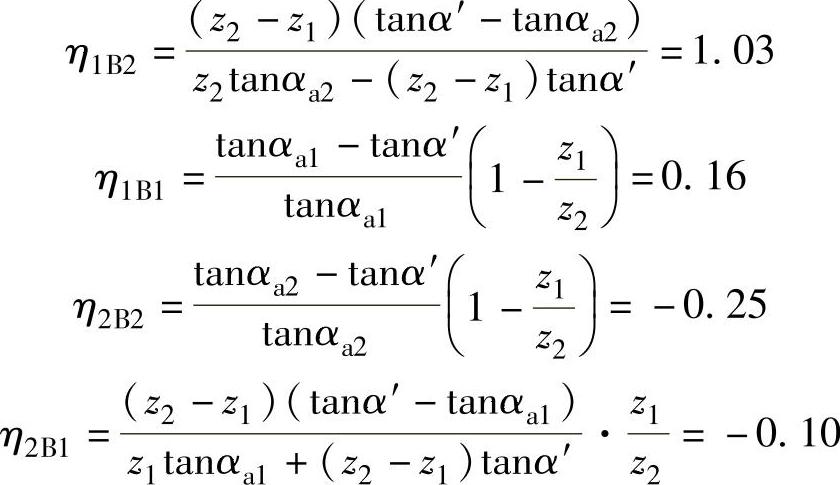
其中α′=α=20°。

由本例计算结果可知，内啮合传动的滑动率在B₂点最大。为了减小滑动率，可以对内齿轮进行正变位，使B₂点向节点P靠近，则B₂点的滑动率便可减小。