一对齿轮啮合时，当前一对轮齿脱开之前，后一对轮齿应当已经进入啮合，这是一对齿轮连续而平稳工作的重要条件。关于这一指标，通常用重合度大于1来表示。

所谓重合度ε_α，是指实际啮合线长度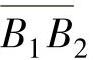与基圆齿距（基节）p_b的比值，即

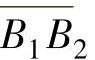称为实际啮合长度，可用齿轮的有关参数表示。由图4-13可知：

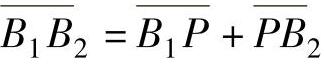，由正弦定律得到

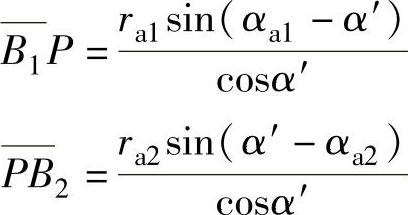
而基节p_b=πmcosα。将各值代入式（4-48）并整理后，便得到

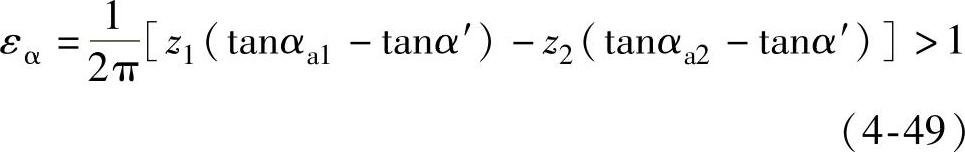(www.daowen.com)

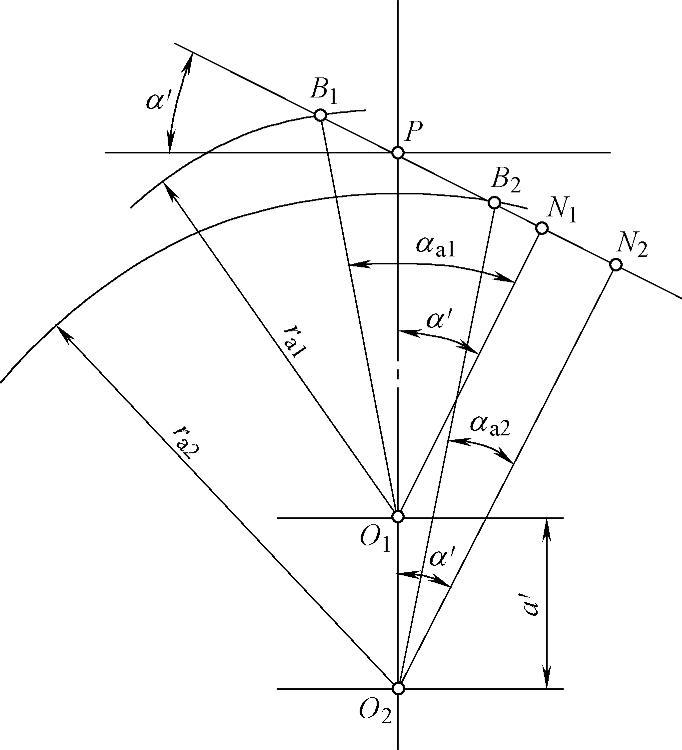
图4-13 重合度的计算

重合度ε_α＞1是保证连续传动的必要条件。对于外啮合传动的重合度ε_α，在设计时应使ε_α=1.1～1.4。内啮合比外啮合的重合度大，一般的标准齿轮或是x_Σ不太大的变位齿轮传动，重合度是能够保证的。只有在齿数差很少的内啮合中，因采用较大的x_Σ，也就是啮合角α′较大，从而使实际啮合线缩短，使重合度明显减小。因此，在内啮合传动中，从理论上分析，重合度也应该大于1。但是对于内啮合齿轮，尤其是少齿差内啮合传动，与啮合的齿相邻的另一对齿，即使尚未进入啮合状态，也是极为靠近的。当齿数多而齿数差很少时更是如此，类似于齿轮联轴器。例如z₁=160，z₂=162，m=1.5mm时，通过计算得知，从节点P算起在齿轮的第三个齿上，同内齿轮之间的啮合弧相隔距离不到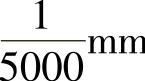。国内有几家单位对多齿接触问题做过试验，证明在啮合瞬时，由于轮齿存在着弹性变形，不止一对齿发生接触，而是同时有几对齿发生接触。华东理工大学用电测法进行动态测试。试验了八台不同参数的少齿差行星减速器接触齿对数。图4-14是其中测试时轮齿根部应力示波曲线。齿轮参数为m=3.5mm，z₁=63，z₂=64，输出转矩T₂=600N·m，重合度ε_α=1.003。

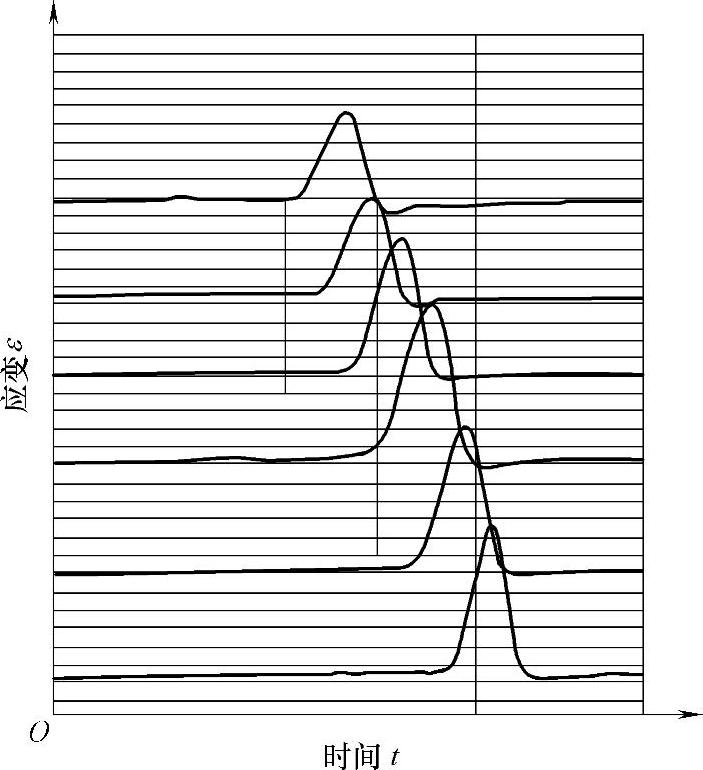
图4-14 动态测试示波曲线

在实际测试中，即使理论重合度ε_α=1.1，模数m=2.25mm，z₁=100，z₂=102，G_s=0.05，瞬时接触齿的对数随着负载的增大竟达至5～6对。国内曾制造过5kN的电动葫芦，采用一齿差内齿轮副，z₁=41，z₂=42，m=3mm，ε_α=0.877。虽然重合度ε_α＜1，但经几万次负载起吊试验，证明符合使用要求。以上事实说明了少齿差内齿轮副重合度即使小于1，也能运行这一现象。但严格来说，多齿接触并不等于多齿啮合。从传动的连续性和平稳性而言，还是希望多对齿啮合，即重合度越大越好。因此，在少齿差行星齿轮传动中，仍将ε_α＞1作为设计要求的条件。