通常内齿轮是用插齿刀加工的，如改变插齿刀与内齿轮毛坯的相对位置，便可加工出变位内齿轮。用刃磨至原始截面（x₀=0）的插齿刀切内齿轮，当插齿刀向外移，使加工中心距a′₀₂大于标准加工中心距（a₀₂=r₂-r₁）时，称为正变位，其变位系数为正值；反之，使加工中心距小于标准加工中心距时，为负变位，其变位系数为负值。为便于分析计算，引用假想标准齿条刀具的概念，把内齿轮齿槽看成外齿轮的轮齿，如图4-1所示。这个外齿轮用假想标准齿条刀具加工，当假想标准齿条刀具中线与内齿轮分度圆离开一段距离，使中心距加大，这时的变位系数x₂（正变位）就作为内齿轮的变位系数，但此变位系数并不代表用插齿刀加工内齿轮时的实际变位量，而只是借用外齿轮的相应公式来计算内齿轮的几何参数及大部分尺寸。

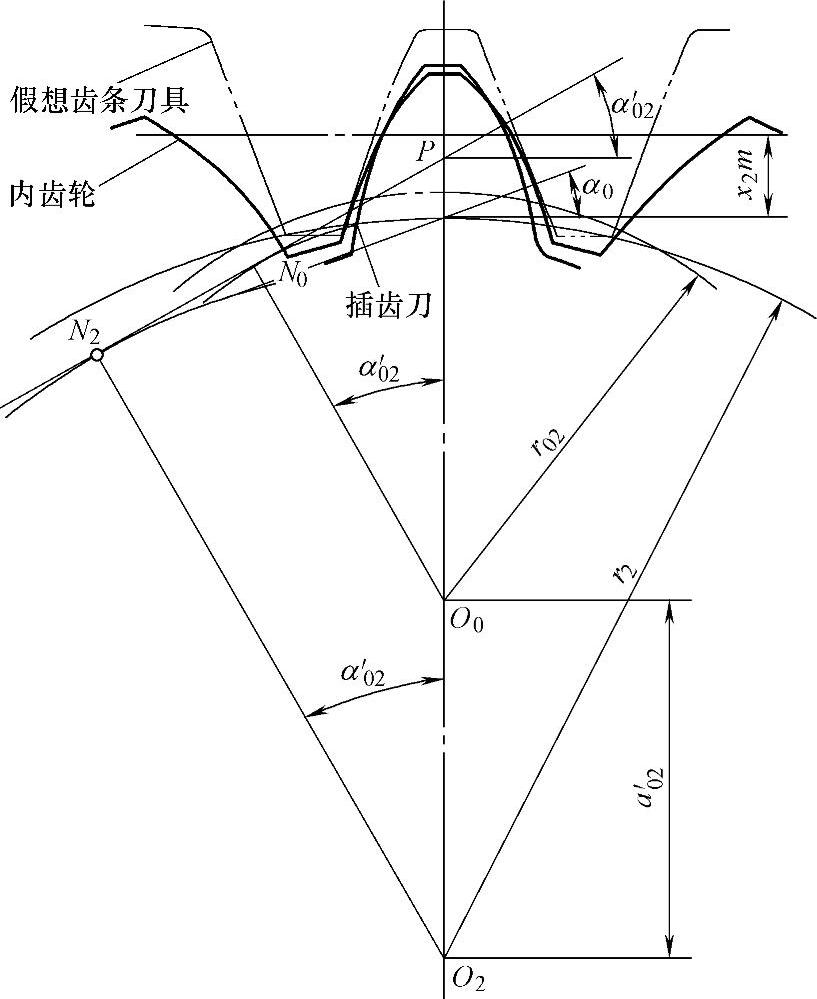
图4-1 变位内齿轮形成原理

正变位时，假想齿条刀具的另一条直线（节线）与内齿轮的分度圆作纯滚动，刀具节线上的齿槽宽减小，因此加工出的内齿轮的分度圆齿厚减薄；反之，负变位时，内齿轮的分度圆齿厚增加。

由于插齿刀齿形为渐开线，不同于齿条型刀具的齿形α=20°的斜线，所以插齿刀加工的变位量H₂≠x₂m，而是H₂=y₀₂m，分度圆齿厚变化量Δs₂与H₂之间关系也不同于齿条型刀具。我们采用假想齿条型刀具来加工内齿轮，目的是可与用齿条型刀具加工外齿轮的几何计算公式相一致，其表达方法较为简单，但与实际情况略有出入。这种计算方法可称为基齿条制。而用插齿刀加工的内齿轮的中心距变动系数y₀₂可由下式求得

式中 α₀′₂——加工内齿轮时，插齿刀与内齿轮的啮合角，。(www.daowen.com)

则内齿轮齿厚的变化量Δs₂=Δ₂m=（z₂-z₀）（invα-invα′₀₂）m，这种计算方法称为基齿轮制。若采用基齿条制，则Δs₂=Δ₂m=2mx₂tanα。而外齿轮Δs₁=Δ₁m=2mx₁tanα，则x₂与y₀₂的关系式如下：

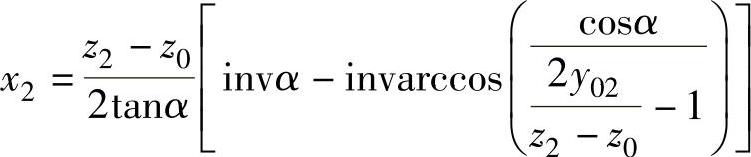
目前国内设计少齿差行星传动，不少采用的是基齿轮制，为了照顾习惯与沿用，本书中的实例中，不少是按基齿轮制设计的。为了与外啮合计算统一，建议还是采用基齿条制，齿厚的实际控制，是由加工检测确定的。

内齿轮的齿根高及齿根圆直径是由插齿刀加工时的中心距a′₀₂决定的。

内啮合齿轮变位传动亦有高度变位及角度变位。高度变位传动中，x₁=x₂≠0，内齿轮分度圆的齿槽宽等于外齿轮分度圆的齿厚，两齿轮的节圆与分度圆重合，两轮中心距等于标准中心距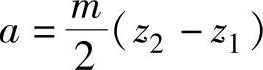，啮合角α′=α（分度圆压力角）。角度变位传动可分为正传动及负传动。正传动中，内齿轮的变位系数大于外齿轮的变位系数，x₂-x₁＞0，两齿轮节圆与分度圆不重合，两轮中心距a′＞标准中心距a，啮合角α′＞分度圆压力角α；负传动中，x_2-x₁＜0，两轮中心距a′＜标准中心距a，啮合角α′＜分度圆压力角α。

在K-H-V型行星传动中大多采用正传动角度变位传动。