双内啮合2K-H（NN）型正号机构少齿差行星传动的传动比计算，可分为下列三种情况：

（1）图3-3所示的传动形式 其结构图如图2-13所示。内齿轮4固定，即n₄=0，内齿轮2与行星外齿轮3连成一体，即n₂=n₃，外齿轮1连同低速轴输出，计算i_H1。

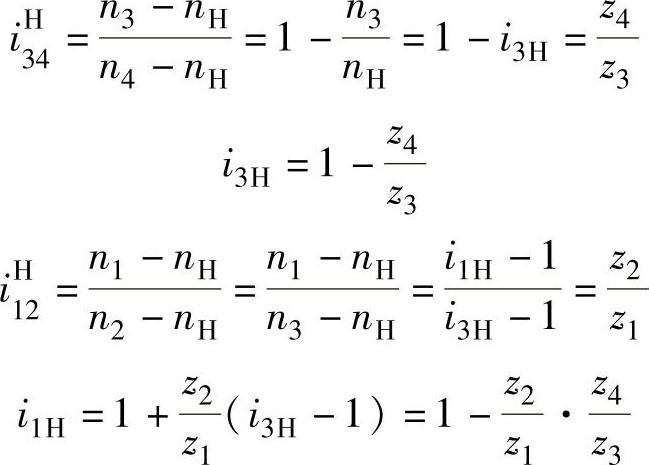
式中，（z₄-z₃）＞0，（z₂-z₁）＞0。

从式（3-3）可知，当齿数差确定后，可调整齿轮1、3，或齿轮2、4的齿数来获得所需的传动比。输入与输出转向相反。

（2）图3-4所示的传动形式 其结构如图2-14所示。外齿轮1固定，即n₁=0，内齿轮2与行星外齿轮3连成一体，即n₂=n₃，内齿轮4输出，则

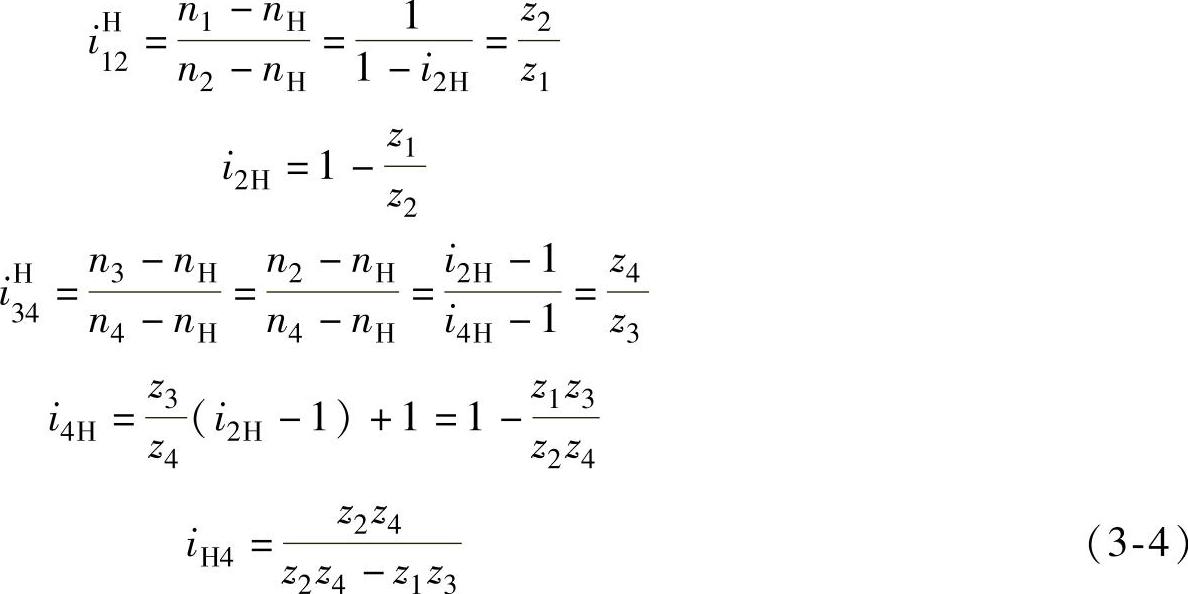
式中，z₄-z₃＞0，z₂-z₁＞0。

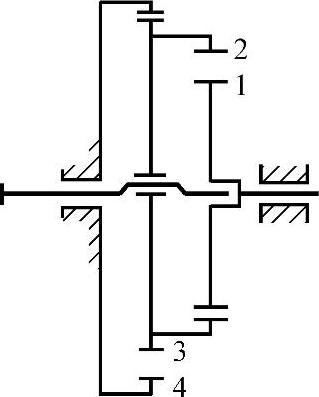
图3-3 2K-H（NN）型传动（内齿轮固定）

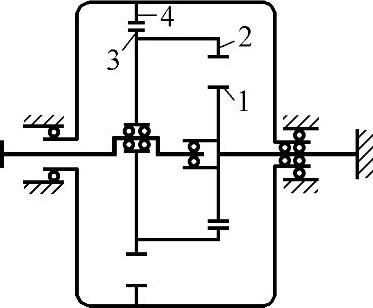
图3-4 2K-H（NN）型传动（内齿轮输出）

从式（3-4）可知，内齿轮4连同机壳输出，输入轴与输出轴转向相同。

（3）图3-5所示的传动形式 其结构图如图3-6所示，内齿轮4固定，即n₄=0，两个行星外齿轮2、3连为一体，即n₂=n₃，内齿轮1作低速输出，其传动比计算式与式（3-3）相似，即

其中z₄-z₃＞0，z₁-z₂＞0。

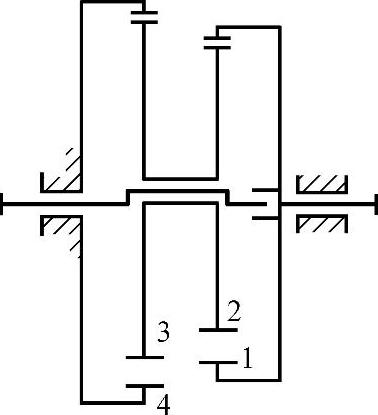
图3-5 2K-H（NN）型传动（以内齿轮工作低速轴输出）

这种传动形式，根据z₁与z₄选取的不同，可设计成输入与输出转向相同或相反。并且可通过搭配使（z₂z₄-z₁z₃）值很小，从而获得比K-H-V（N）型减速装置更大的传动比。

若两对齿轮的模数相同时，则齿数差一般也取相同值，即均为z_∑，这样容易得到相同的中心距。

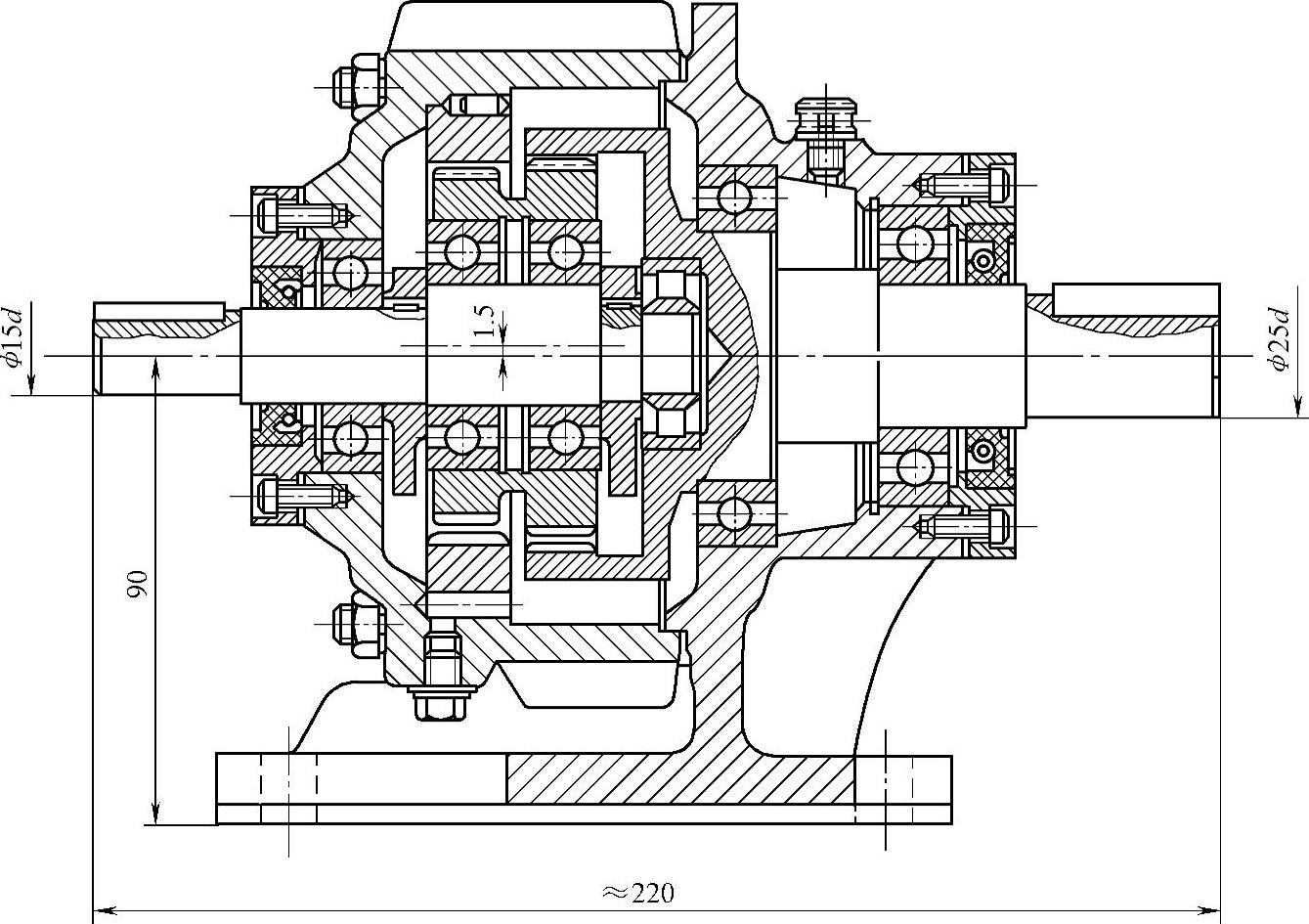
图3-6 2K-H（NN）型传动（以内齿轮输出）结构图

对于图3-5所示的传动机构，输入轴与输出轴的转向关系确定方法如下：当两对齿轮的齿数差相同时，式（3-5）中的z₁z₃-z₂z₄=z₁（z₄-z_∑）-z₂z₄=z_∑（z₄-z₁），当z₄＞z₁时，则i_H1＞0，即n_H与n₁的转向相同；当z₄＜z₁时，i_H1＜0，即n_H与n₁的转向相反。

设计时，往往是根据已知的传动比i_H1来确定四个齿轮的齿数。若完全用试凑法，则盲目性太大。下面介绍一种计算方法。

取z₄-z₃=z₁-z₂=z_∑，z₄-z₁=z₃-z₂=z_e，则式（3-5）可写成

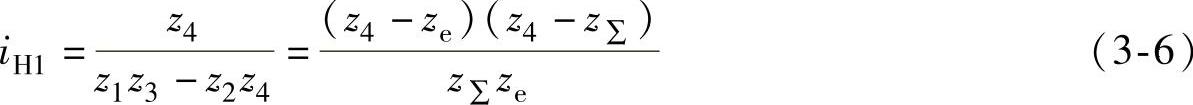
若i_H1、z_∑和z_e已知，上式中只有z₄是未知数，故可以求出z₄。将式（3-6）整理后求根，得到z₄的计算式为

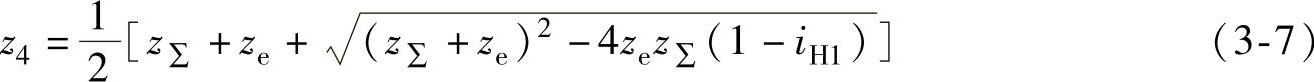
但应注意，在z_e=0时，式（3-7）不适用。

【例3-2】 已知i_H1=200，z_∑=2，z_e=4，求各齿轮齿数。

解 按式（3-7）求z₄，即

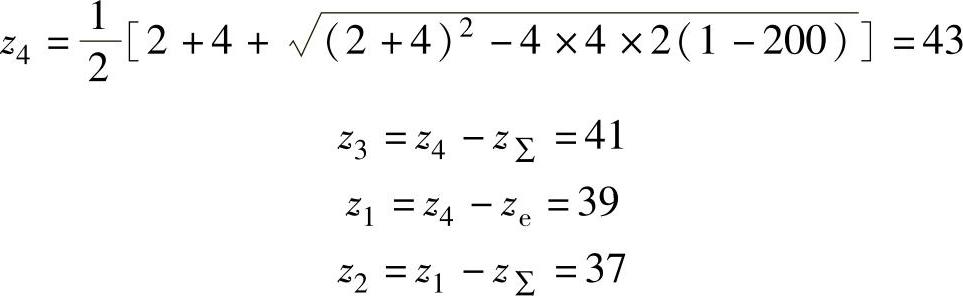
验算传动比(www.daowen.com)

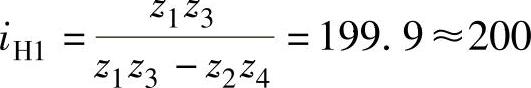
【例3-3】 已知i_H1=-200，z_∑=2，z_e=-4求各齿轮齿数。

解 按式（3-7）求z₄，即

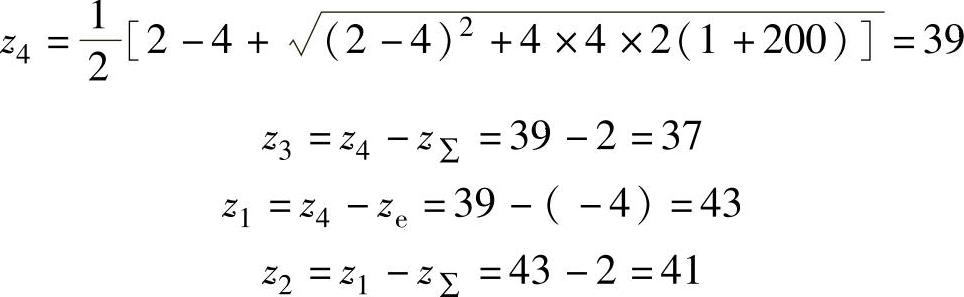
验算传动比

i_H1=-198.9

为了使z₄的计算式再简单一些，当z₄＞z₁，即z_e＞0时，可取

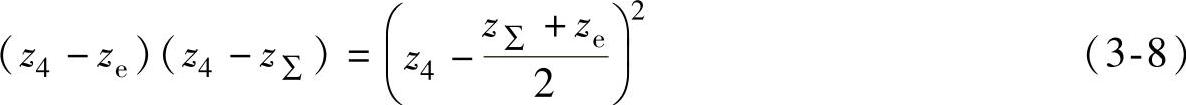
则

【例3-4】 用式（3-9）计算例3-2中的z₄。

解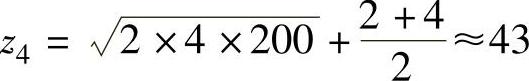

结果与用式（3-7）计算得出的结果相同。当z_∑及z_e改变时，用两种计算式计算的结果也可能出现不大的差异。

此方法是南京自动化技术研究所提出的。

当z₄＜z₁即z_e＜0时，尚无较准确的简单近似计算方法。

外齿轮输出的2K-H（NN）型少齿差行星传动（见图3-3），其传动比计算为

式（3-10）与式（3-3）相同，由于z₄＞z₃及z₂＞z₁，故i_H1值小于零，则n_H的转向始终与n₁的转向相反。

根据已知的传动比确定各齿轮齿数的方法如下：

由式（3-10）得到

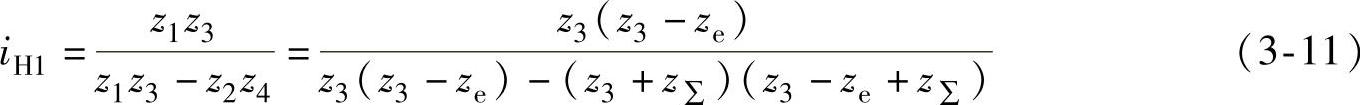
当i_H1、z_∑和z_e已知时，式中只有z₃为未知数，故可以求出z₃。

将式（3-11）整理后求根，得到z₃的计算式为

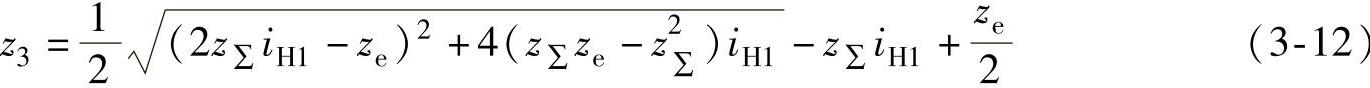
【例3-5】 已知i_H1=-50，z_∑=1，z_e=10，求各齿轮的齿数。

解 将各值代入式（3-12）得

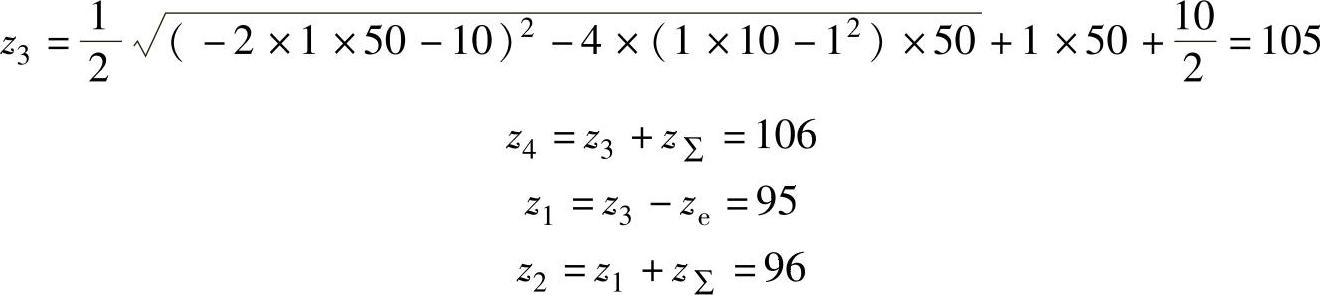
验算传动比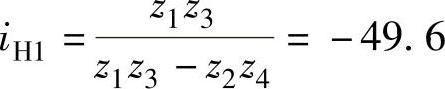

以下将应用上述方法确定齿数的有关注意事项加以说明。

1）由于在最初计算齿数z₄（或z₃）时只取整数部分，故最后应验算实际的传动比。若用于计数机构，其传动比需要完全准确，如果计算结果发现传动比达不到设计要求，则需用试凑法计算。若用于一般的传动，只要传动比误差在允许范围内即可。

2）因为在模数一定时，齿数越多则径向尺寸越大，所以当发现齿数不合适时，可改变z_∑和z_e再重新计算。

3）当内齿轮齿数太少时，可能给选取插齿刀带来困难。这时也应改变z_∑及z_e再重新计算。

4）计算时，传动比及z_e均应带着正负号代入计算式。

根据瑞士ACBAR大传动比减速器系列及日本一项测试报告而得到的相同结论，为了获得尽可能高的效率，当传动比大于28时，应当采用内齿轮输出，如图3-5所示的形式；而当传动比小于28时，应当采用外齿轮输出的形式，如图3-3所示的形式。上述传动比均是指绝对值而言。