1.对R_i和r₀的尺寸分析

当取定碟形高度h=D_i/4时（相当标准椭圆形封头），碟形封头可能有各种不同式样，如图12-11所示。

1）图12-11所示最上面曲线：maxR_i⇒∞；有maxr₀且等于h，球面部分成为平板，受力最差。

2）图12-11所示最下面曲线：有minR_i及minr₀，且minr₀=0。碟形封头成为球缺，受力也差。

3）介于上述两极端情况之间，可有无数的球面半径和转角半径的组合。

分析图12-11可知：当球面半径最大（∞）减小至最小minR_i时，转角由maxr₀减小至最小minr₀=0，其比值R_i/r₀也由无穷大减少到某一最小值再回到无穷大。

显然，当R_i/r₀值是最小时，所得的碟形封头最近似于椭圆形封头，其受力状态比较接近椭圆形封头。此最小比值min（R_i/r₀）就是所寻找的优化值，使应力增强系数M最小，封头壁厚最薄。

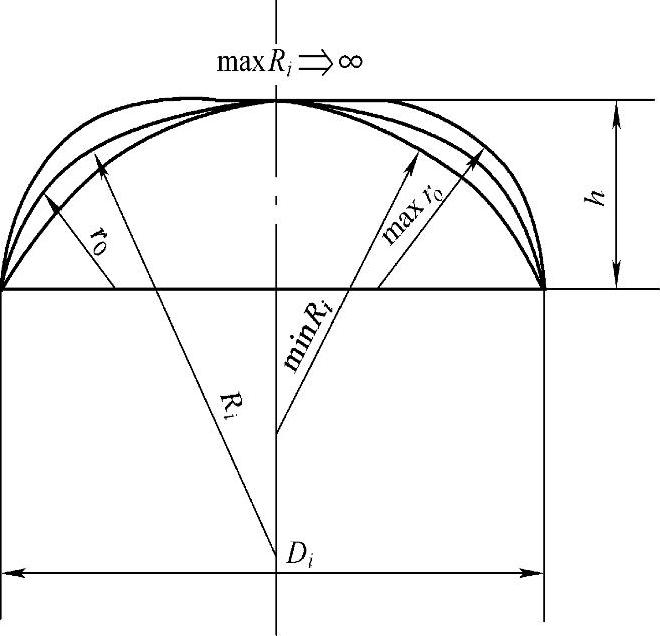
图12-11 碟形封头各种可能的半径R_i和r₀的变化

2.R_i/r₀的优化值

（1）几何关系给定参数：直径D_i，高度h=D_i/4；设计变量R_i/r₀。

由图12-10所示，几何关系：

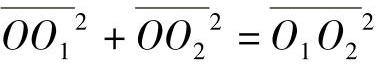
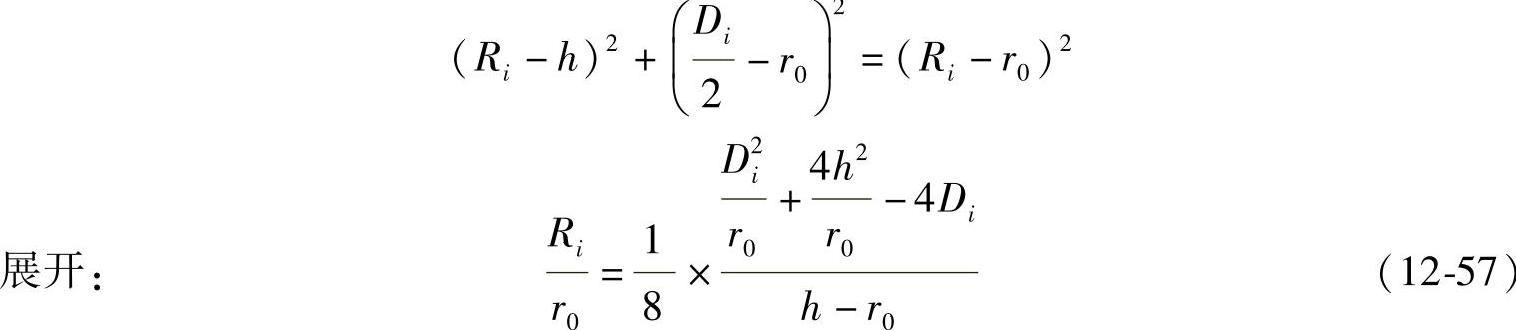
代入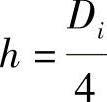，得

（2）优化数学模型与结果 目标函数：

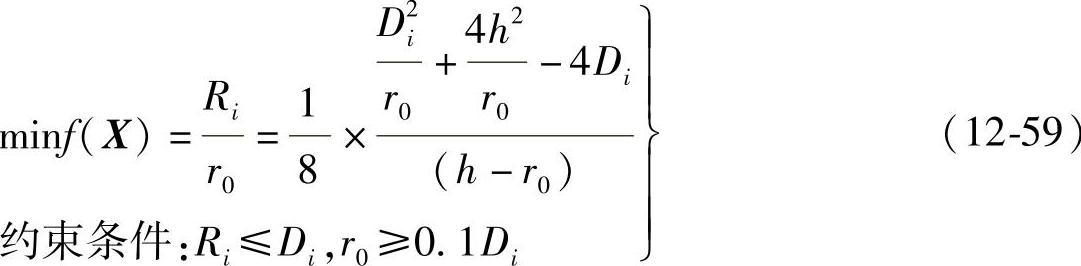
用计算机和优化设计程序软件，即可求出R_i/r₀的最小值，见表12-5。(www.daowen.com)

表12-5 碟形封头优化后的尺寸

3.求导方法确定R_i/r₀的极小值

对式（12-58）求一阶导数，得两个极值点：

D_i=5.79r₀ （12-60a）

D_i=2.21r₀ （12-60b）

分析式（12-60b），D_i=2.21r₀，即r₀=0.452D_i。过渡区转角半径过大，封头太高，制造困难。同时在公切点a处的边缘弯曲应力迅速衰减后，使过渡区承受薄膜的环向压应力，受力差，故舍弃r₀=0.452D_i的极值。

保留式（12-60a），即：r₀=0.173D_i。将r₀=0.173D_i代入式（12-58）得R_i/r₀=5.24，并得到R_i=0.905D_i。

碟形封头优化比较，见表12-6。

表12-6 碟形封头优化后比较

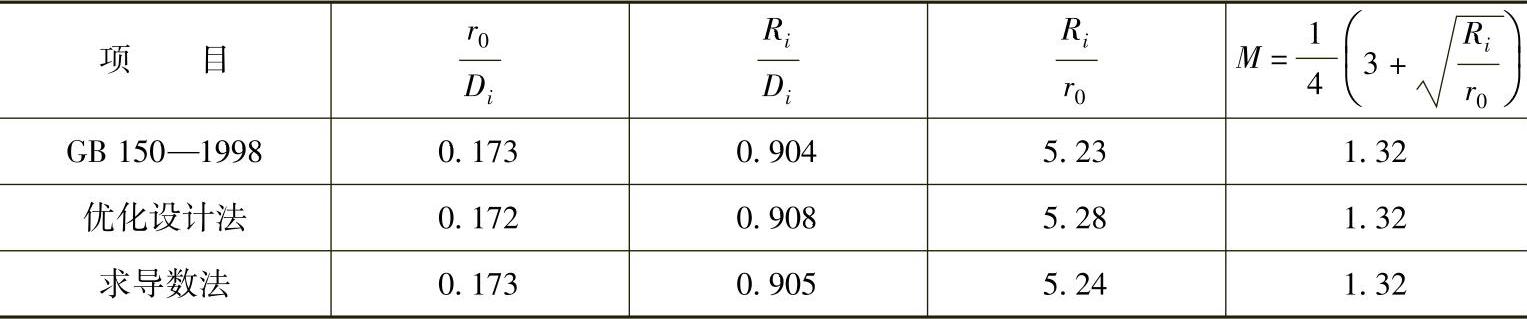
说明GB150—1998《钢制压力容器》提供的数据范围：r₀/D_i=0.06→0.173；R_i/D_i=1.0→0.904，只有r₀/D_i=0.173，R_i/D_i=0.904这组数据，才是min（R_i/r₀）=5.23时所对应的最优尺寸。

4.碟形封头优化尺寸系列

以求导数方法确定的极小值min（R_i/r₀）=5.24为准，当取R_i≤D_i的不同值时，r₀也有相应值，见表12-7。

表12-7 碟形封头优化尺寸系列（h=D_i/4）

表中数据有实用价值，可供工程设计使用。