1.设计变量

法兰是和容器或管道直接相连的，其内径D_i及颈部小端有效厚度δ₀一般等于容器或管道的内径和壁厚，故设为定值；螺栓孔直径d_b、螺栓个数、螺栓材料在常温下的许用应力[σ]_b、焊接颈部高度h₁参照现行标准确定；法兰外径可由法兰的公称压力、公称直径及螺栓规格查JB/T 4701～4707—2000得到；垫片压紧力作用中心圆直径D_G可由所取的垫片尺寸计算得出。取法兰有效厚度δ_f、锥颈大端有效厚度δ₁和锥颈高度h作为设计变量，同时，在设计中涉及到的设计温度下的极限强度S、内压p也作为随机参数进行处理，构成随机变量组：

X=[x₁，x₂，x₃，x₄，x₅]^T=[δ_f，δ₁，h，s，p]^T （12-12）

并假设它们均服从正态分布。法兰的结构尺寸如图12-2所示。

图12-2 整体法兰结构尺寸图

2.目标函数

若以整体法兰质量最小为优化目标，则目标函数可写成：

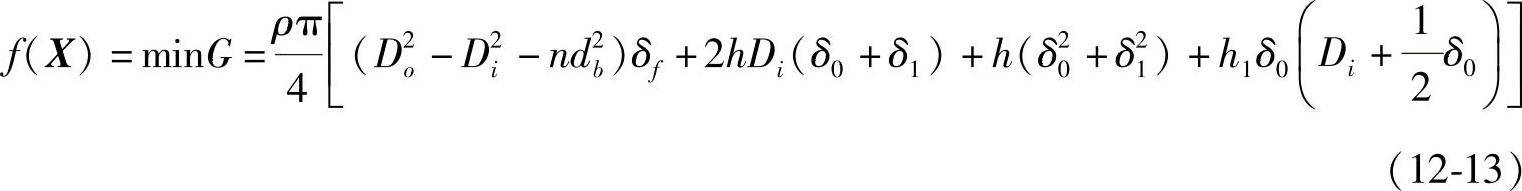
式中 G——法兰质量（kg）；

ρ——法兰材料密度（kg/m³）；

D_i——法兰内径（mm）；

D_o——法兰外径（mm）；

d_b——螺栓孔直径（mm）；

δ₀——法兰颈部小端有效厚度（mm）；

δ₁——法兰锥颈大端有效厚度（mm）；

δ_f——法兰有效厚度（mm）；

h——法兰锥颈高度（mm）；

h₁——法兰焊接颈部高度（mm）。

D_b、D_G、LD、LT、LG、L的具体意义如图12^-2所示。(www.daowen.com)

3.约束条件

根据Waters法，整体法兰的3种主要应力为σ_H、σ_R、σ_T，假设它们满足法兰材料的极限强度要求，并设其可靠度分别为R₁、R₂、R₃。强度约束方程如下：

对正态分布函数，有

所以约束方程转化为

同理有

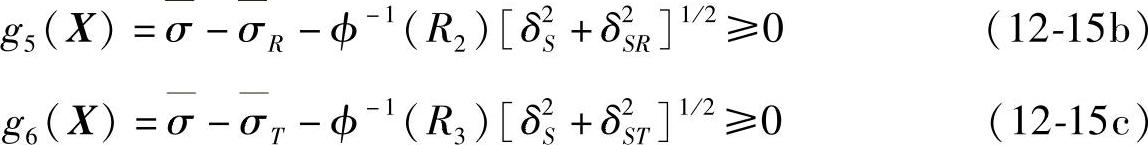
式中 ϕ^-1（x）——标准正态累计分布函数的反函数；

σ——设计温度下法兰材料屈服强度的均值（MPa）；

σ_H——法兰颈部轴向应力的均值（MPa）；

σ_R——法兰环径向应力的均值（MPa）；

σ_T——法兰环切向应力的均值（MPa）；

δ_SH——法兰颈部轴向应力的方差（MPa）；

δ_SR——法兰环径向应力的方差（MPa）；

δ_ST——法兰环切向应力的方差（MPa）；

δ_S——设计温度下法兰材料屈服强度的方差（MPa）。