不同的机械零部件的危险应力和失效模式各有不同，但其可靠性设计可以采用相同的数学力学模型，如应力强度干涉模型法。由于数学力学模型相同，在本质上所计算的精度应大体相同，这为推广可靠性设计带来了光明的前景。根据Back方法，采用拟梁结构模型，对于整体法兰（图12-1），可求得在D₁直径上，即危险截面处的弯应力为

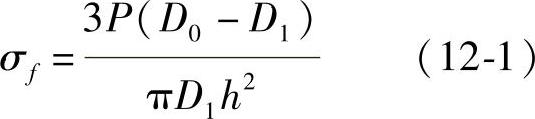
式中 P——法兰受力的总和（Pa）；

D₀——螺钉分布圆的直径（mm）；

D₁——危险截面的直径（mm）；

h——法兰的厚度（mm）。

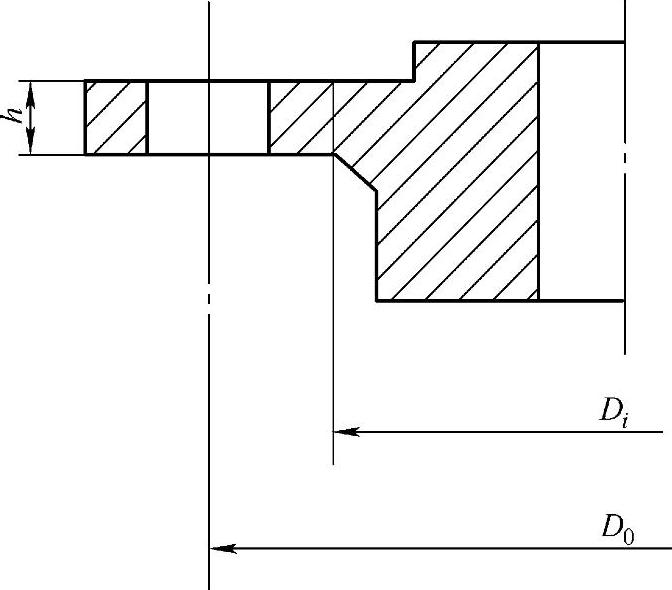
图12-1 整体法兰

根据应力-强度干涉理论，以应力极限状态表示的状态方程为

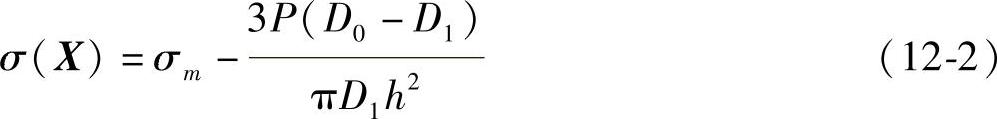(www.daowen.com)

式中 σ_m——法兰的材料强度（MPa）；

X——基本随机变量向量，X=（σ_m，D₀，D₁，h，P）T。这里基本随机变量向量X的均值E（X）和方差Var（X）是已知的，并且可以认为这些随机变量是服从正态分布的相互独立的随机变量。σ（X）为状态函数，可表示零部件的两种状态：

这里极限状态方程σ（X）=0是一个五维曲面，称为极限状态或失败面。

可靠性指标定义为

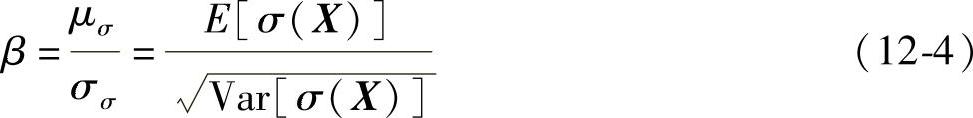
式中 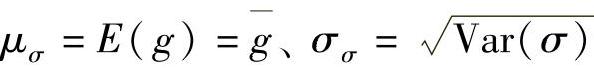——分别是状态函数σ（X）的均值与标准差。

这样，一方面可以利用可靠性指标直接衡量构件的可靠性，另一方面在基本随机参数向量X服从正态分布时，可以用失败点处状态表面的切平面近似地模拟极限状态表面，可以获得可靠度的一阶估计量：

R=ϕ（β） （12-5）