1.残余预应力

扁平绕带压力容器截面结构尺寸如图11-8所示。设钢带层共有m层，钢带的预应力用矢量[T]={T₁，T₂，T₃，…，T_m}表示。其中的T_k为第k层钢带的预应力。由[T]引起的径向外压可以写成矩阵[p^r]：

[p^r]=S_rcos²α[T][R]^-1 （11-47）

式中 [p^r]——因钢带缠绕而引起对已缠好筒体的径向应力矩阵（MPa）；

S_r——钢带的厚度（mm）；

α——钢带相对于环向的缠绕倾角（°）；

[R]，R₁，R₂，…，R_m——分别为几何矢量，内筒第1，2，…，m层钢带的内半径（mm）。

设第k层钢带的内径为R_k，则由式（11-47）便可求得容器绕制完成后的残留预应力。计算时将绕制好的筒体（内筒和已缠绕完成部分）作为承压实体，计算外面缠绕钢带时在这部分实体上的应力。应力计算采用拉美公式，则残留预应力[σ_r]_pre、[σ_t]_pre和[σ_z]_pre分别为

[σ_r]_pre=[L^r][p^r]^T=S_rcos²α[L^r][R]^-1[T]^T（11-48）

式中 [σ_r]_pre——因钢带缠绕引起的径向应力（MPa）；

[L^r]——按拉美公式改写的径向外压承力矩阵。

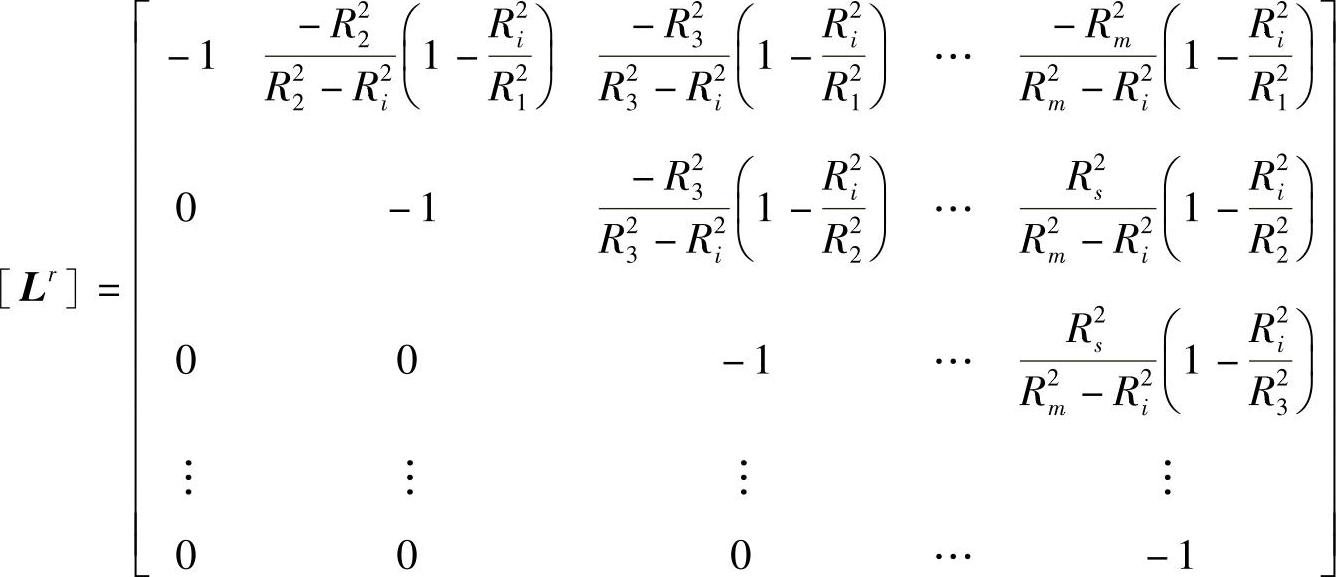
同理有

[σ_t]_pre=[N][T]^T+[L^t][p^r]^T={[N]+S_rcos²α[L^t][R]^-1}[T]^T （11-49）

式中，

式中 [L^t]——按拉美公式改写的环向外压承力矩阵。

同理有：

[σ_z]_pre=[L^z][p^z]^T （11-50）

式中 [p^z]——因钢带缠绕而引起对已缠好筒体的轴向应力矩阵（MPa）。

[p^z]=sin²α[T](www.daowen.com)

式中 [L^z]——按拉美公式改写的轴向外压承力矩阵。

2.内压作用下的最终应力

显然，只要将绕带容器作为厚壁容器，按绕带容器的应力计算公式计算出筒体的应力分布，然后与上节计算得的残留预应力进行叠加，就可以得最终应力，这里内压[p]为常数，故可写成：

[σ_r]_p=[M^r][p]^T （11-51）

式中 [σ_r]_p——因内压引起的径向应力（MPa）；

[M^r]——按拉美公式改写径向内压承力矩阵；

p——设计内压力（MPa）。

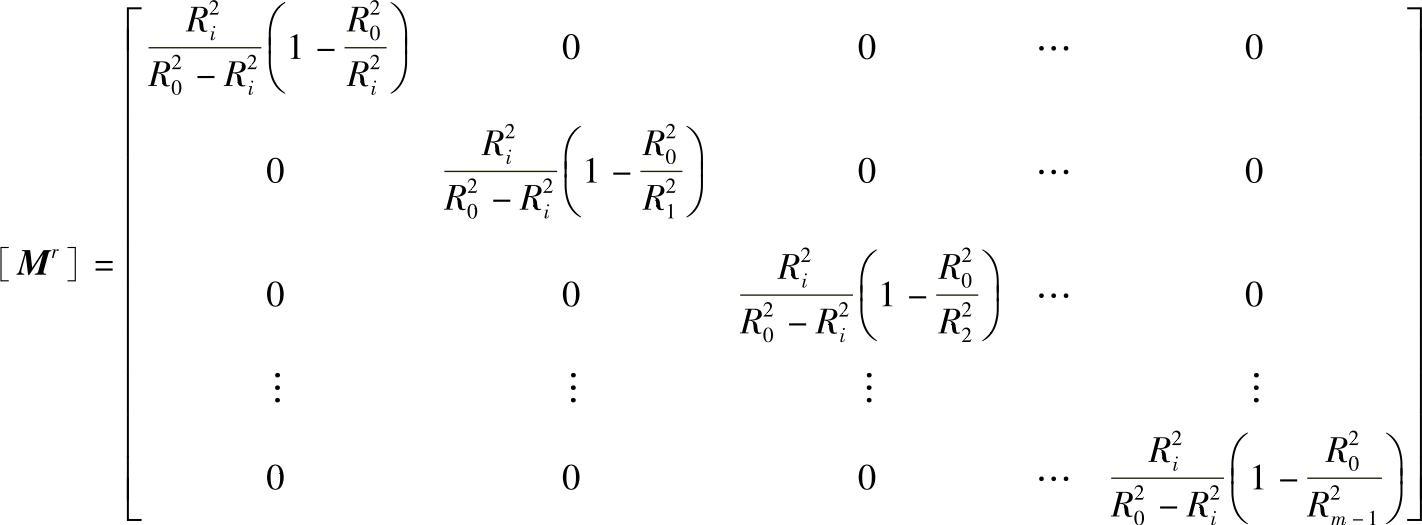
同理有

[σ_t]_p=[M^t][p]^T （11-52）

式中 [σ_t]_p——因内压引起的环向应力（MPa）；

[M^t]——按拉美公式改写环向内压承力矩阵。

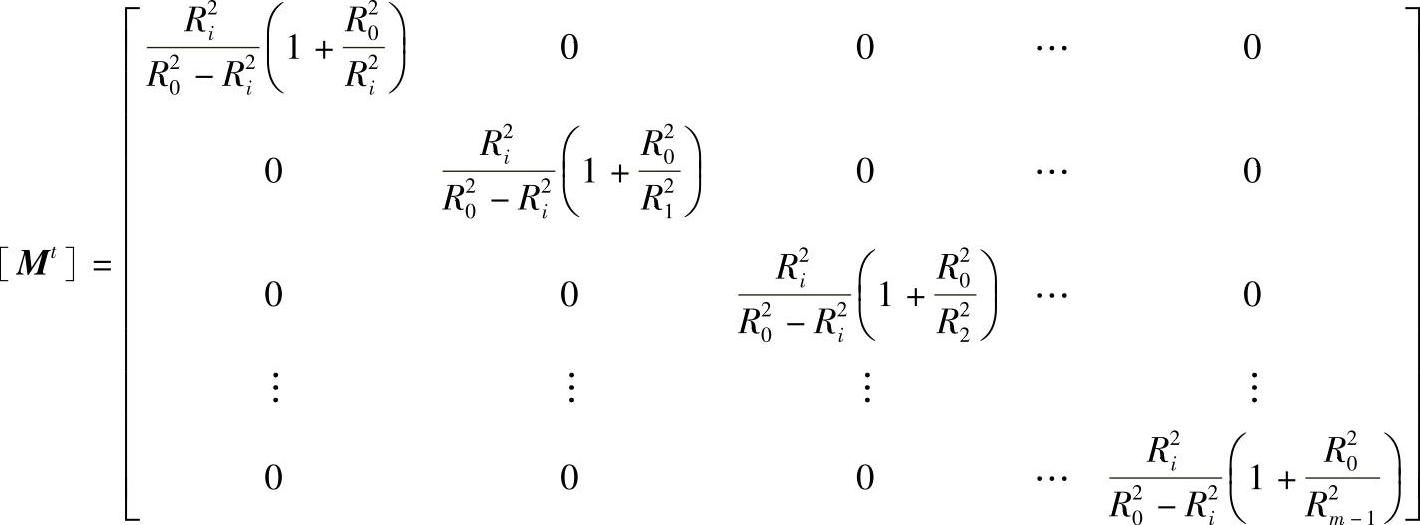
同理有

[σ_z]_p=[M^z][p]^T （11-53）

式中 [σ_z]_p——因内压引起的轴向应力（MPa）；

[M^z]——按拉美公式改写轴向内压承力矩阵。

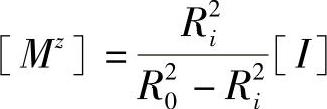
由式（11-48）、式（11-49）、式（11-50）与式（11-51）、式（11-52）、式（11-53）叠加以后，即可得最终筒体应力为