模糊优化模型求解的基本原理为寻求一最优水平截集，将模糊优化模型等价转化为最优水平截集上的常规优化模型处理。与最优水平截集对应的最优水平阈值，即为模糊约束的最优隶属度，现以某合成塔设计为例，了解模糊优化模型的求解过程。

1.采用二级模糊综合评判法确定最优水平阈值

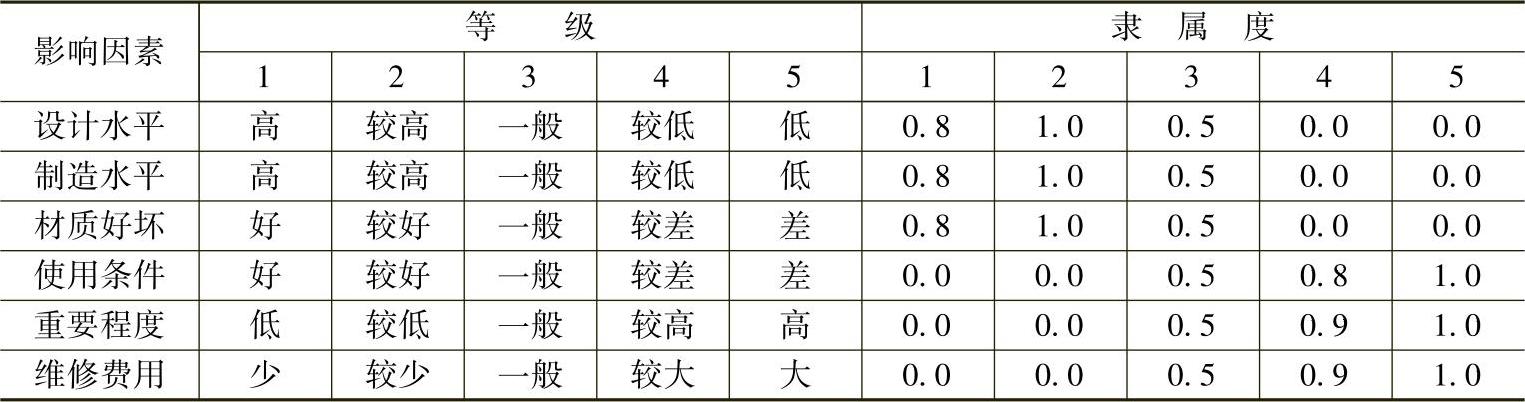
最优水平阈值λ^*、影响λ^*取值的因素、因素等级和隶属度见表11-3，表11-3中的隶属度是采用专家打分法确定。

表11-3 影响因素、因素等级及其隶属度

2.确定备择集

选定的评判对象是截集水平值λ，其取值范围是[0，1]区间。备择集为

λ={0.30，0.40，0.50，0.60，0.65，0.70，0.75，0.80，0.85，0.90}

3.确定权重集

为了准确反映各因素及因素等级对评判对象λ的影响，应赋予各因素及因素等级以不同的权重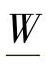和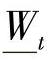，根据设计条件可确定权重集：(www.daowen.com)

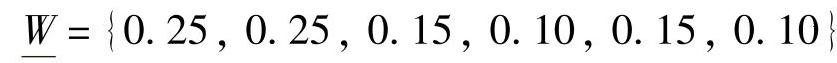
4.进行二级模糊综合评判

由模糊矩阵乘法得到评判结果为

B=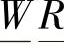（0.0799，0.19337，0.33，0.53，0.66，0.80，0.876，0.9266，0.85，0.547）

由加权平均法求最优水平阈值λ*为

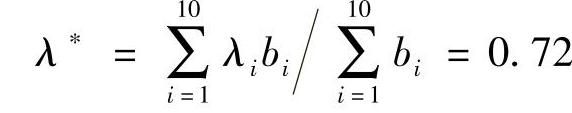
从而将模糊优化问题转化为常规优化问题。

5.选择常规优化方法求解

由上分析可知，多层包扎式厚壁圆筒的模糊可靠性优化设计问题是以质量为目标函数，在模糊可靠性约束下寻找最小质量。由于参数较少，优化方法可选用复合形法。