一般由计算压力在圆筒上所产生的应力被认为近于正态分布，其概率密度函数为

式中 μ、s——分别为应力变量x的均值和标准差。

与上述对应的许用应力[σ]作为模糊变量处理，其模糊性用隶属函数来表示，模糊隶属函数为降半梯形分布时，其表达式为

式中 σ（x）——应力对许用应力的隶属度；

a₁、a₂——许用应力，用扩增系数法确定为a₁=0.95[σ]+0.05[σ]（1_-λ^*）、a₂=[σ]+0.05[σ]（1-λ^*），其中最优水平阈值λ^*的求解见11.3.3。

式中 ϕ（x）——标准正态分布函数。

若要求设计的可靠度为R，则可靠度设计法则为

1.设计变量

设计变量为多层包扎圆筒内筒名义壁厚δ_i、多层包扎圆筒层板层总厚度δ₀，即

2.目标函数

设计目标为多层包扎式厚壁圆筒的质量最小，则目标函数的数学表达式可写为

f（X）=minW=πρL（D_ix₁+D_ix₂+2x₁x₂） （11-14）

式中 ρ——材料密度（kg/m³），取7.8×10³ kg/m³；

L——圆筒直段长度（mm）。

3.约束条件

（1）圆筒计算模糊可靠度约束条件 用可靠性函数y=f（x₁，x₂，x₃）建立约束条件时，其均值μ_y、标准差S_y和变异系数为

即s_x1=C_xiμ_x1 （11-17）(www.daowen.com)

式中

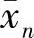——随机变量的均值；

s_xi——随机变量的标准差；

C_xi——随机变量的变异系数，计算压力C_pc=0.05，圆筒C_Di=0.005，有效厚度C_δo=0.005，C_c=0.005厚度附加量。

计算应力σ^t的均值和标准差

将p_c、D_i和δ_e=x₁+x₂-C代入式（11-15）～式（11-17），得

将μ_δt、s_δt和多层包扎圆筒的[σ]^tφ代入式（11-10），求出模糊可靠度R₁，则内筒轴向强度的约束条件：

g₁（X）=R₂-R₁≤0 （11-18）

（2）几何约束条件 内筒壁厚一般取12～25mm，则

g₂（X）=12-x₁≤0 （11-19）

g₃（X）=x₁-25≥0 （11-20）

层板层总厚度一般取6～8N mm（N为层数），则

g₄（X）=16N-x₂≤0 （11-21）

g₅（X）=x₂-12N≤0 （11-22）

至此，多层包扎式厚壁圆筒的模糊可靠性约束条件的数学模型已经建立，约束条件还可根据工作要求的变化而改变。