优化设计以减轻结构质量为目标，以结构不失效为原则，即达到安全和经济的统一。本节中以壁厚最小为优化目标，以各层缠绕角为设计变量。考虑到压力容器以渗漏为失效判据，故本节中以最大应变准则作为约束条件，建立优化模型：

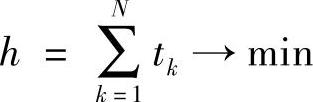
约束条件：

式中 k——第k层；

N——总层数；

t_k——单层厚度（mm）；

α_k——第k层缠绕角（°）；

{e_L^（k）}——第k层应变限定值列向量。

层合板的应变公式（11-1）中，包含了铺层厚度和各层缠绕角。这是一个十分复杂的关系，包含三角函数四次方分式的数列求和，优化设计已是非常复杂。当温度场因素介入后，更加复杂。这是由于：

1）复合材料层合板热应力应变关系本身就十分复杂。

2）铺设厚度h确定之前，不但铺设层数无法确定，温度场也无法计算。(www.daowen.com)

3）如果给定一个厚度初始值h₀，以此计算出温度场分布，然后通过温度场和层合板受力状态结合，反算的厚度h₁必然与其初始值h₀有差异。进而又将使温度场分布也发生变化，又导致新的厚度。

为了对优化模型求解，本节中用惩罚函数法与单纯型法结合的方法。首先对原优化模型加工成无约束优化模型：

f（X）=h+aR（h，α_k）→min （11-7）

式中 a——惩罚因子；

R——惩罚函数。

当设计变量满足约束条件时，R（h，α_k）=0，否则R（h，α_k）＞0。显然，当a充分大时，f只能在R（h，α_k）=0时取得极小值。而此时式（11-7）与原优化模型目标函数相同，设计变量也能满足原优化模型的约束条件。所以式（11-7）与原优化模型当a充分大时是等价的。

为了避免求解厚度与缠绕角的复杂关系，优化过程把厚度也作为一个设计变量输入。同时输入惩罚因子a，然后求解无约束优化模型（11-7），得出各层缠绕角α_k和容器壁厚h。如果得出的α_k、h满足式（11-6）的约束条件，则停止计算，所得α_k、h即为最优解。否则，用得出的α_k，h作为初值，并增大惩罚因子a，重新求解式（11-7），直到得出最优解。计算框图如图11-1所示。

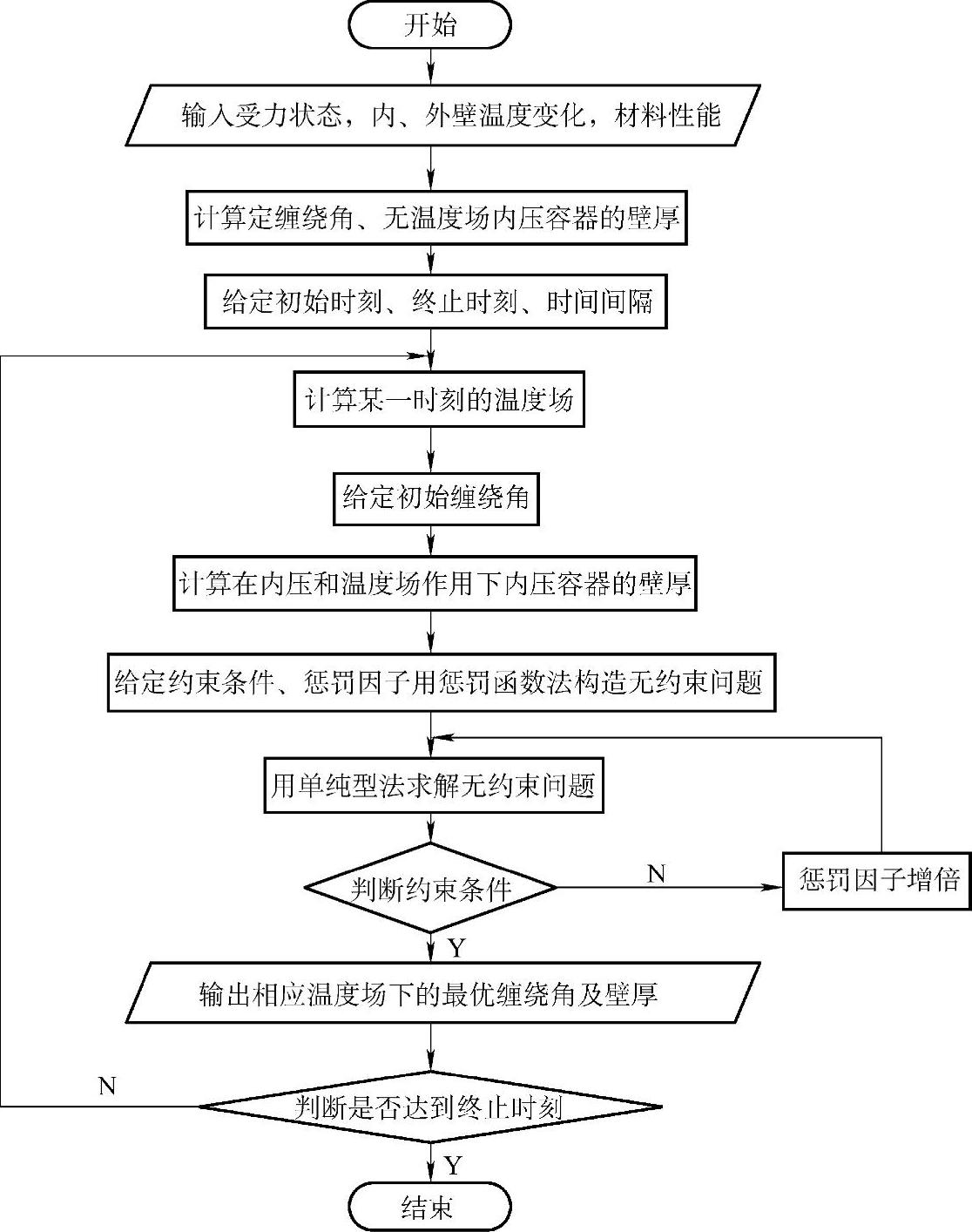
图11-1 程序流程图