1.已知条件

某高压容器设计压力p=16MPa，设计温度t=200℃，材料16MnR，筒体内半径R₁=775mm，筒体壁厚δ₁=100mm，封头的内半径R₂=800mm，封头厚度δ₂=48mm。在设计温度下，筒体的许用应力S^c_m=140MPa，封头的许用应力S^s_m=150MPa。优化设计过渡段削边长度L，使过渡区最大应力水平系数最低。

2.应力状态分析

因主要讨论封头与筒体过渡区应力状况，故忽略封头上其他结构，建立如图10-6所示的有限元分析模型。有限元计算采用ANSYS提供的8节点四边形单元PLANE82。L=94mm时计算结果如图10-7所示。

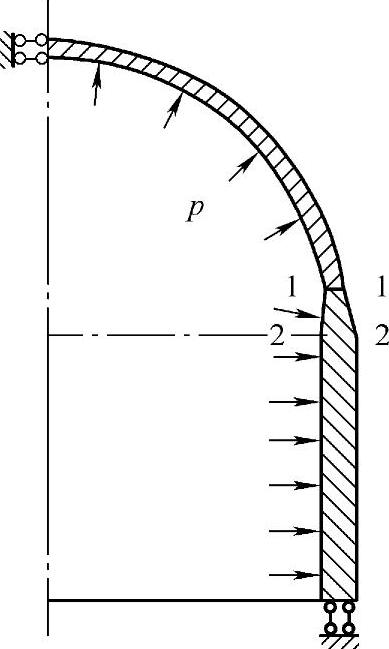
图10-6 有限元分析模型

图10-7 应力云图

由图10-7所示，最大应力强度出现在封头与过渡区连接线的内壁。为此将封头与过渡区连接线取为第一条应力处理线，同时将筒体上封头切线位置取为第二条应力处理线（图10-6）。并利用ANSYS的GET命令提取每一条路径上的各应力分量σ_x、σ_y、σ_z及τ_xy，根据各应力分量计算主应力，按第二强度理论计算应力强度一次局部薄膜应力P_L以及一次弯曲应力P_b与二次应力Q三者之和，并根据分析设计应力评定条件按下列各式计算截面1-1和2-2的应力水平系数。

以削边长度L为设计变量，一般取：

L≥3y （10-69）

式中，y=max{（R₁+δ₁）-（R₂+δ₂），R₂-R₁} （10-70）

由式（10-69）及式（10-70）得L≥81mm。L的上限应根据内壁可削边长度L₁及外壁与封头相切原则所确定的外壁削边长度L₂来确定（图10-5），并取较小者。(www.daowen.com)

则L_max=min（L₁，L₂）=198.4mm，即削边长度L≤198.4mm。

3.优化设计数学模型

应力水平约束条件为

β^i-i，ξi-i≤1（i=1，2） （10-73）

以连接区最大应力水平系数最低为优化目标，取设计变量为L，可确定高压容器球形封头与筒体连接区优化设计的目标函数为

s（L）=max（β^1-1，ξ^1-1，ξ^2-2，ξ^2-2） （10-74）

4.优化过程及结果分析

分析时，首先选用ANSYS提供的等步长搜索法（SWEEP）锁定优化区间，由于ANSYS限定每次搜索的步数不超过10，因此，需将整个区间分成若干个子区间进行搜索。等步长搜索法得到的目标函数与设计变量L的关系如图10-8所示。可见，最优削边长度L在81～100mm，当L超过100mm时，目标函数随L增大而明显增大。

经等步长法搜索后，利用ANSYS提供的零阶方法进一步寻优，并将削边长度L限定在81～100mm。所谓零阶方法是指只用到目标函数值与状态函数值而不用它们的导数。程序首先利用惩罚函数法将有约束优化问题转换为无约束优化问题，然后利用最小二乘拟合函数逼近法寻优。根据零阶方法得到最优削边长度为95mm，对应此结构的各应力水平系数分别为β^1-1=0.574，ξ¹_i-1=0.316，ξ_o^1-1=0.239，β^2-2=0.592，ξ²_o-2=0.400，ξ²_i-2=0.267。各系数的下角标i表示内壁，o表示外壁。

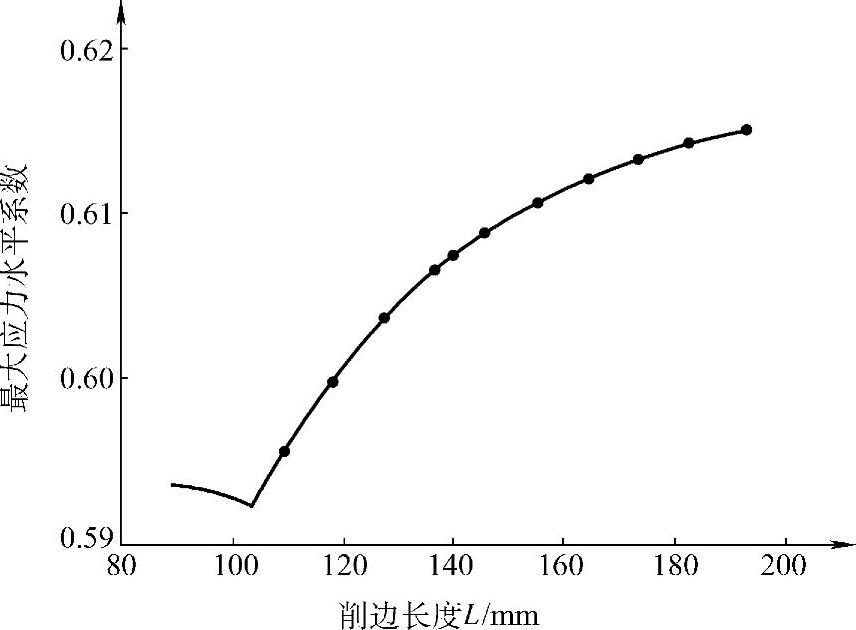
图10-8 最大应力水平系数与削边长度之间的关系

综上所述，基于分析设计建立高压容器球形封头与筒体连接区的优化数学模型，利用有限元程序ANSYS提供的参数化设计语言A PDL及优化模块OPT进行优化计算，从而实现压力容器不连续区分析设计意义上的优化设计，优化后可使不连续区应力水平最低，为高压容器此类不连续区的安全运行提供必要的保障。