1.决策变量

由上述分析可知，问题的决策变量为：弹-塑界面半径r_c；表示壁厚的径比k₀。参数为：弹性模量E、E_t；力学性能σ_s、σ_b；内径r_i；设计压力p_i。

由于使用的高压容器材料结构的不同选择，故参数E、E_t、σ_s、σ_b是在适用的结构材料所给定的一组值内选取。

2.约束条件

（1）不发生反向屈服条件 根据福贝尔（Faupel）应用材料的屈服强度求出容器的允许最大超应变度χ_max，卸压后容器不会产生反向屈服，其表达式为

σ_s=5350（χ-16.8），χ≤χ_max （10-59）

（2）最佳超应变度条件 按10.4.4中的分析可知，在容器设计时弹-塑界面半径应选择满意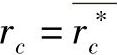，由式（10-58）可知：

（3）强度条件 由于目前国内尚无超高压容器的设计规范，故按日本HPIS_- C-10—1980《超高压圆筒容器设计指针》中的规定，容器在强度上应满足：

式中 f_s——安全系数，f_s=f₀×f₁，考虑载荷条件的变化，检验技术及质量管理等因素，f₀取1.5以上，f₁为有关可靠性的安全系数；(www.daowen.com)

σ_b——材料的强度极限（MPa）。

（4）爆破压力约束 按福贝尔爆破压力公式并检验安全系数，应有

安全系数：

n_b=（p_b/p_i）≥2.5 （10-63）

（5）几何尺寸约束

r_i≤r_c≤r₀，r_i≤r₀≤3r （10-64）

综上所述可知，目标函数为

约束条件为式（10-59）～式（10-64），决策空间是二维的，而参数空间则是六维的。