把设计压力（即工作压力）下引起的筒壁应力与残余应力叠加求得其相当应力，在（E_t/E）p_a-p_i＞0的条件下，可以证明其具有下列性质：

1)对任一给定的r_c、σ_eq(X)为变量的函数，则σ_eq1(X)是单调增凹函数，σ_wq2(X)为单调减凸函数，X=(r，r_c)，图形如图10-3所示。

2)当r=r_c时，有σ_eq1(X)=σ_eq2(X)，把r=r_c代入式(10-55)和式(10-56)，则有

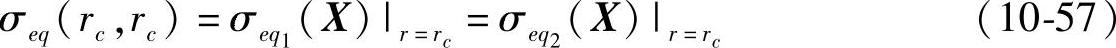
易求得函数σ_eq(r_c，r_c)的最小点r_c=r_c^*，即

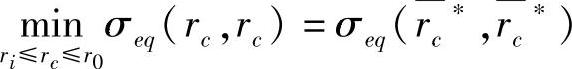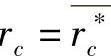对于由和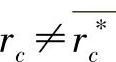所确定的应力分布可证明有下列的性质：

3)对在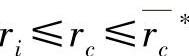内任一给定的r_c，则有

①若r_i≤r≤r_c，则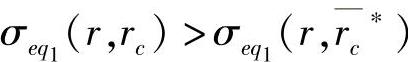；②若r_c≤r≤F_c^*，则曲线σ_eq2(r，r_c)与曲线σ_eq1(r，r_c^*)有交点；③若r_c^*＜r＜r₀，则σ_eq2(r，r_c)＜σ_eq2：(r，r_c^*)。

4)对在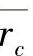＜r_c≤r₀内任一给定的r_c，则有

①若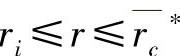，则σ_eq1(r，r_c)＜σ_eq1(r,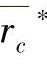)；②若r_c^*＜r≤r_c，则曲线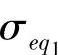(r，r_c)与曲线σ_eq2(r，r_c^*)有交点；③若r_c＜r≤r₀，则σ_eq2(r，r_c)＞σ_eq2(r，r_c^*)。性质1）～4）的图形如图10-3和图10-4所示。

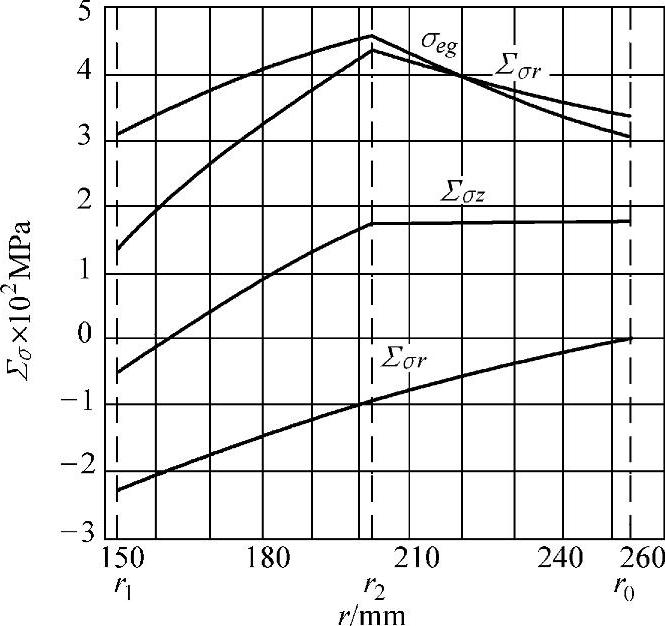
图10-3 工作压力下的合成应力和相当应力(www.daowen.com)

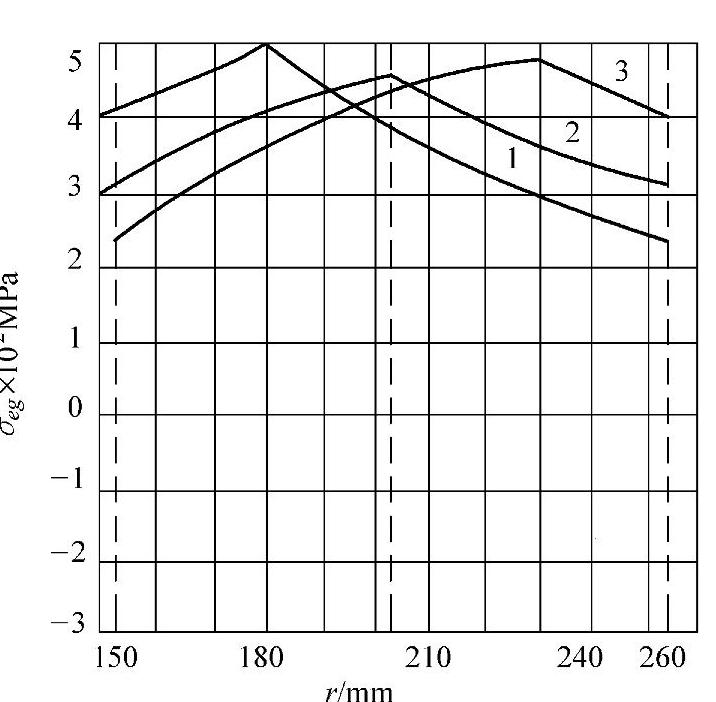
图10-4 弹一塑界面半径r_c取不同值时叠加应力的相当应力函数σ_eq(r，r_c)

l—r＜r_c^* 2—r_c=r_c^* 3—r_c＞r_c*r_c=152.5mm，r₀=254mm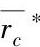，=203mm

关于叠加应力的相当应力函数给m下面两个定义：

定义1 若存在r_c=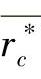，使σ_eq(r，r_c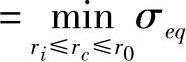^*)(r，r_c)成立，其中r_i≤r≤r_a，则称r_c=r_c^*为叠加应力的相当应力函数σ_eq(X)的绝对最优解。

定义2 若函数σ_eq（r_c，r_c）在区间（r_i，r₀）内有最小点r_c=r_c^*存在，即

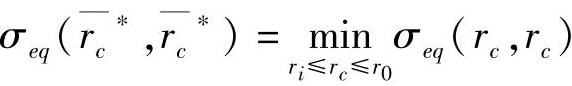
成立，则称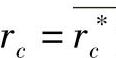为叠加应力的相当应力函数σ_eq（X）的满意解。

由上述性质1）～4）可证明如下定理：

定理 叠加应力的相当应力函数σ_eq（X）的绝对最优解不存在，但存在且有唯一的满意解。