1.设计变量

高压容器往往是细长结构、两端的封头多为半球形，如图10-1所示。因此，壳体的质量可由容器内径D_i、筒体长度L、筒体壁厚δ₁及封头厚度δ₂等参数来确定；在一定设计条件下，由内径D_i和筒体长度L可确定壳体壁厚δ₁及封头壁厚δ₂。因此可以选择高压容器的形状尺寸D_i、δ₁、δ₂作为设计变量，即

X=[x₁，x₂，x₃]^T=[D_i，δ₁，δ₂]^T （10-1）

2.目标函数

高压容器壳体质量等于圆筒部分的质量与球形封头部分的质量之和。圆筒部分质量为

M₁=ρπ（D_i+δ₁）Lδ₁ （10-2）

高压容器的两个半球形封头的质量为

M₂=3ρπ（D_i+δ₂）²/2 （10-3）

高压容器壳体的总质量为

M=M₁+M2

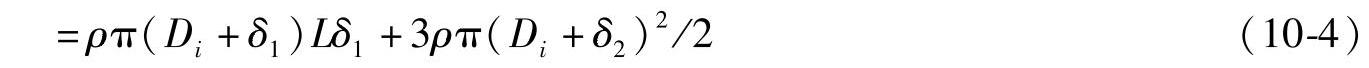
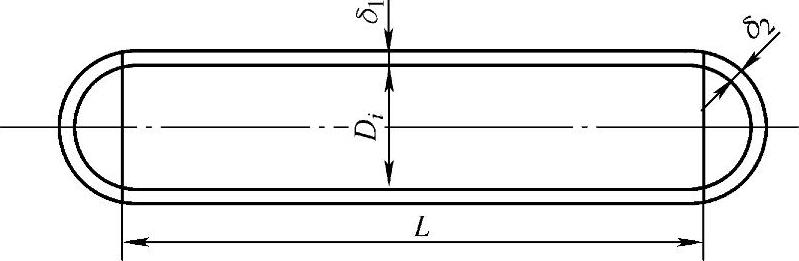
图10-1 高压容器示意图

高压容器的全容积为

由此可得

代入式（10-4）得高压容器的目标函数，即壳体的质量为

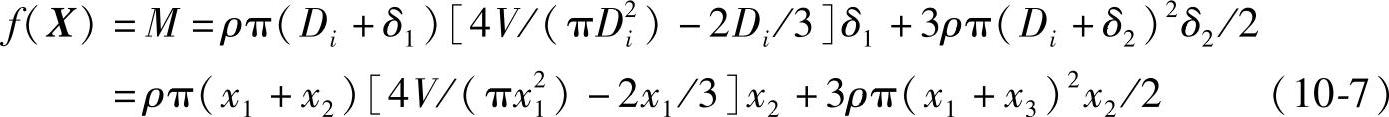
式中 ρ——材料密度（kg/m³），取ρ=7.85×10³kg/m³；

D_i——筒体内径（mm）；

V——圆筒全容积（mm³）；

L——筒体长度（mm）；

δ₁——筒体的计算壁厚（mm）；

δ₂——球形封头的计算壁厚（mm）。

3.约束条件

（1）强度条件GB 150—1998《钢制压力容器》规定，当设计压力低于35MPa时，高压容器圆筒和球形封头的壁厚可由中径公式计算，即(www.daowen.com)

根据式（10-8）和式（10-9），可得

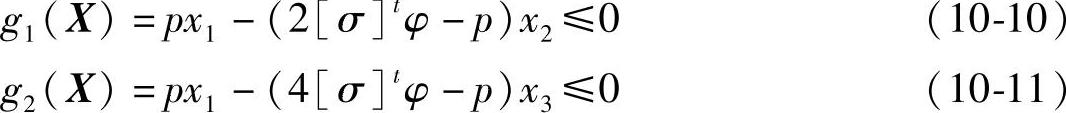
式中 p——容器的计算压力（MPa）；

[σ]^t——高压容器制造材料在设计温度下的许用应力（MPa）；

φ——容器的焊缝成形系数。

（2）长径比条件 高压容器由于承受压力较高，容器内径的增加将使容器的壁厚显著增加，从而使容器的质量增加；另外，由于容器的直径增加，将导致容器的密封困难。因此，在设计时，一般将容器的长度和直径之比进行限制，通常取长径比

写成约束标准形式，即

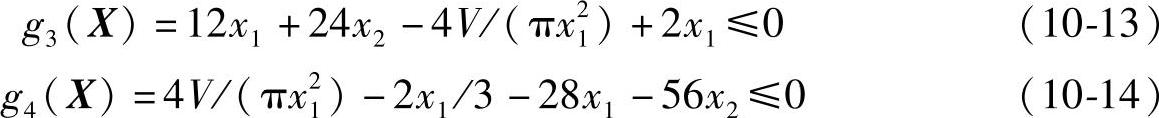
（3）外内径之比条件 外内径之比K可以间接反映高压容器在承压时应力沿壁厚的分布情祝。在同等压力作用下，K值越大，应力沿器壁分布的不均匀程度越大。所以，为了使应用中径公式计算的结果不致于和实际结果之间存在过大的偏差，通常对高压容器的外内径之比进行限定。我国规定高压容器的外内径之比K应满足以下条件：

写成标准约束形式，即

g₅（X）=2x₂-0.5x₁≤0 （10-16）

（4）非负性条件

g₆（X）=-x₁≤0 （10-17）

g₇（X）=-x₂≤0 （10-18）

g₈（X）=-x₃≤0 （10-19）

根据上面的分析，可得出基于高压容器的最小质量为目标函数的优化设计的数学模型为

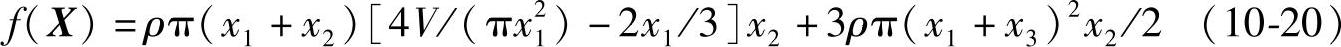
约束条件：g₁（X）=px₁-（2[σ]^tφ-p）x₂≤0

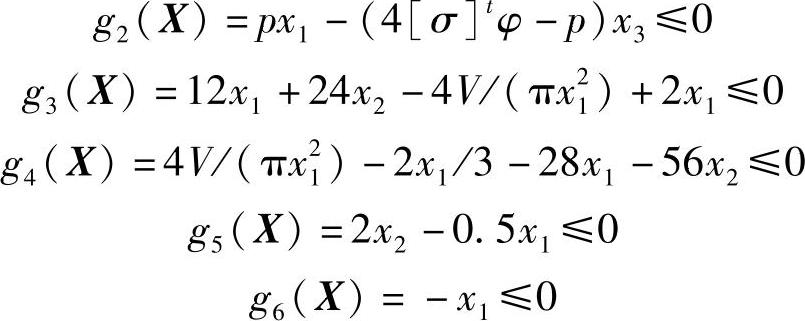
g₇（X）=-x₂≤0

g₈（X）=-x₃≤0

这是一个带有8个不等式约束的三维优化问题，可选用相关优化软件求解。