一般说来，模糊优化模型求解的基本原理为寻求一最优水平截集，将模糊优化模型等价转化为最优水平截集上的常规优化模型处理。与最优水平截集对应的最优水平阈值λ^*即为模糊约束的最优隶属度。现以某减压塔设计为例，阐述模糊优化模型的求解过程。

1.采用二级模糊综合评判法确定最优水平阈值

影响水平阈值λ*取值的因素、因素等级和隶属度见表9-2。表中隶属度是采用专家打分法确定。

表9-2 影响因素、因素等级及其隶属度

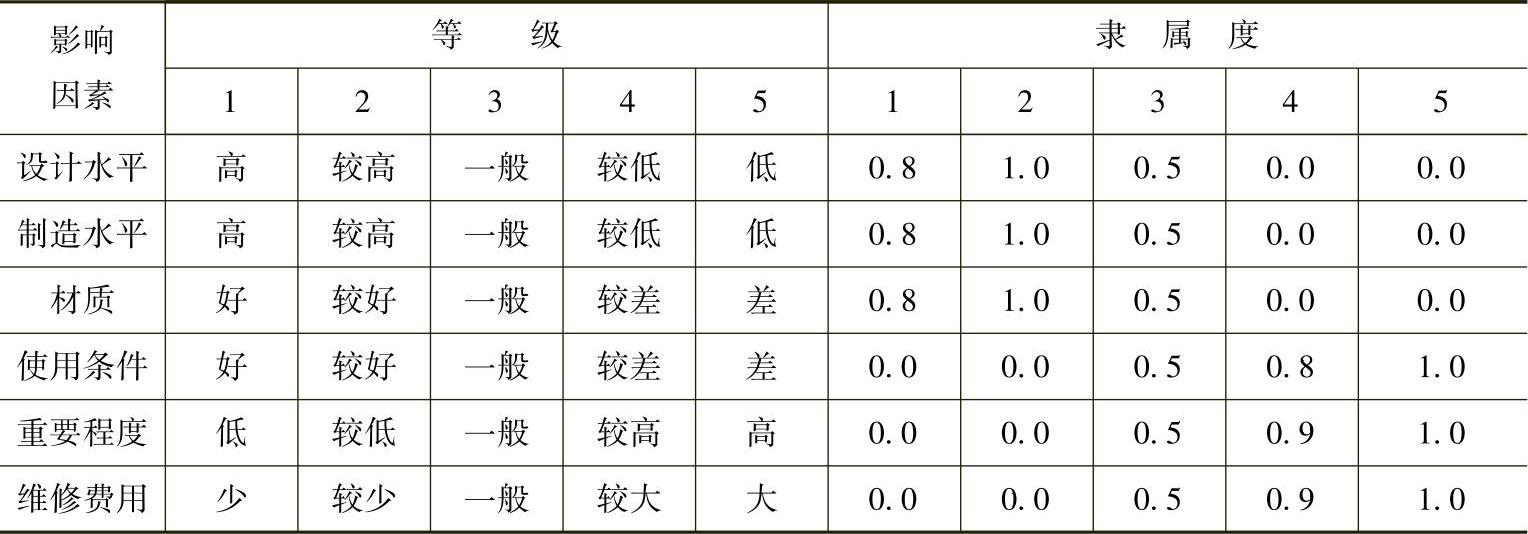
2.确定备择集及权重集

选定的评判对象是截集水平值λ，其取值范围在[0，1]区间。备择集为

λ={0.30，0.40，0.50，0.60，0.65，0.70，0.75，0.80，0.85，0.90}

为了准确反映各因素及因素等级对评判对象λ的影响，应赋予各因素及因素等级以不同的权重W和W_i，根据设计条件可确定权重集：

W={0.25，0.25，0.15，0.10，0.15，0.10}(www.daowen.com)

3.进行二级模糊综合评判

由模糊矩阵乘法得到评判结果为

B=W·R=（0.0799，0.19337，0.33，0.53，0.66，0.80，0.876，0.85，0.547）由加权平均法求最优水平阈值λ^*为

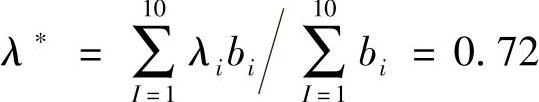
代入式（9-50）的α₁、α₂公式中，从而将模糊优化问题转化为常规优化问题。

4.选择优化方法求解及计算结果对比

由以上分析可知，外压容器模糊可靠性优化设计问题是以质量为目标函数，在模糊可靠性约束下寻找最小质量。由于参数较少，优化方法可选用复合形法。

减压塔塔体内径D_i=6000mm，设计外压力p=0.1MPa，塔体圆筒总高L_z=8000mm，两端为标准椭圆形封头，长短轴的比值为D_i/2H_i=2，工作温度为370℃，材料20g，壁厚附加量C=3mm，塔身设置3个扁钢加强圈，圆筒和加强圈的稳定安全系数m=3，封头的稳定安全系数m=15，设计可靠度R=0.9999，通过模糊可靠性优化，计算塔壁厚度、椭圆形封头厚度及加强圈的尺寸及塔减压的总质量。常规设计按设计手册，经几次试算，得筒体有效壁厚δ_e=7mm、封头有效壁厚δ_e1=7mm、加强圈扁钢80mm×20mm，有效横截面积A_s=1375cm²，总质量约4.009t；经模糊可靠性优化设计结果为筒体有效壁厚δ_e=6mm、封头有效壁厚δ_e1=6mm、加强圈扁钢100mm×10mm，有效横截面积A_s=732.6cm²，总质量约3.371t。比较两种结果可以看出，筒体、封头和加强圈的优化壁厚比原设计壁厚有一定的减少，优化后质量比原设计质量可以减轻16%左右。