如前所述，对于约束问题的优化方法现采用间接法来处理，也可以采用直接法。前者的基本思想是：按照一定的原则，构造一个包含目标函数和约束条件（函数）的新目标函数，从而将约束优化问题转化为无约束优化问题，然后采用一种无约束优化方法进行求解。根据以上加强圈拟优化的数学模型特征，采用惩罚函数法（Sequential Unconstrained Minimization Techniques，简称SUMT法）进行优化计算。

（1）使用外点惩罚函数法对原目标函数进行改造，构造一个新函数，也称为增广目标函数，其形式如下：

式中 M^（k）——惩罚参数。它是一个大于零的递增序列，即0＜M⁰＜M¹＜M²＜…，并可以证明limM^（k）=∞。其值由M^（k+1）=CM^（k）确定；

C——递增系数，一般取：C=5～10；

f（X）——原目标函数，f（X）=3.14x₁x₂ρ；

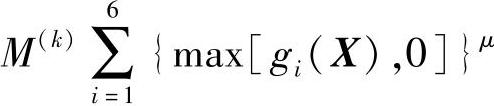——惩罚项函数，它是由惩罚参数M（k）和约束函数通过特定的方式构造起来的；

μ——指数，μ≥1；当采用无约束的直接法的优化方法时，可取μ等于1；当采用无约束的解析法的最优化法的方法时，通常取μ等于2。本例取μ=2。

（2）外点惩罚函数法的迭代寻优过程

1）确定有关参数：初始惩罚参数M^（0）=1；收敛判别精度ε₁、ε₂均应大于零。本例取ε₁=0.1、ε₂=0.01，递增系数C=8；初始点X（M^（0））取在可行域内或外均可。

2）从X（M^（k-1））点出发，采用一种无约束优化方法（本例采用“最速下降法”）求解新目标函数minF（X，M^（k））的优化点和优化解F[X^*，（M^（k））]。其中，

首先，按最速下降法，计算增广目标函数在初始点X（M^（k））（本例K=0）的梯度，即(www.daowen.com)

以及X（M^（k））点的搜索方向，即负梯度方向

式中，分母项为目标函数梯度的模。

其次，检验是否满足收敛判别条件：

若满足以上两式，则停止迭代，X^*（M^（k））即为约束优化解。

否则，应转入3）。

3）改变惩罚参数，即取M^（k+1）=CM^（k），并沿负梯度方向作一维搜索，以确定最优步长的大小，即按下式求出最优步长a^（k）：

并求新点X^（k+1），即

令k=k+1，转入2）重新进行迭代计算，直到满足以上收敛判别条件为止。至此，可求出优化解X^*（M^（k））。

（3）计算程序 用外点惩罚函数法求算优化解的计算程序框图（略）。